This page was generated from a Jupyter notebook. You can view it on GitHub or download and run it locally.
Generalized Hyperbolic (GH) Distribution
The Generalized Hyperbolic distribution is the most general form of the normal variance-mean mixture family.
Definition
A random variable \(X\) follows a Generalized Hyperbolic distribution if it can be written as:
where:
\(Z \sim N(0, \Sigma)\) is independent of \(Y\)
\(Y \sim \text{GIG}(p, a, b)\) (Generalized Inverse Gaussian)
Special Cases
Distribution |
GIG Parameters |
Mixing Distribution |
|---|---|---|
Variance Gamma |
\(b \to 0\), \(p > 0\) |
Gamma\((p, a/2)\) |
Normal-Inverse Gaussian |
\(p = -1/2\) |
InverseGaussian\((\delta, \eta)\) |
Normal-Inverse Gamma |
\(a \to 0\), \(p < 0\) |
InverseGamma\((-p, b/2)\) |
Hyperbolic |
\(p = 1\) |
GIG\((1, a, b)\) |
Key Properties
Joint distribution \(f(x, y)\) is an exponential family
Marginal distribution \(f(x)\) is NOT an exponential family
Fitting uses the EM algorithm with parameter regularization
[1]:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from scipy import stats
from normix.distributions.mixtures import (
GeneralizedHyperbolic, JointGeneralizedHyperbolic,
VarianceGamma, NormalInverseGaussian, NormalInverseGamma
)
from normix.utils import (
plot_joint_distribution_1d, plot_marginal_distribution_2d,
validate_moments, print_moment_validation,
fit_and_track_convergence, plot_em_convergence,
test_joint_fitting, print_fitting_results
)
plt.style.use('seaborn-v0_8-whitegrid')
%matplotlib inline
print("Imports successful!")
Imports successful!
1. Joint Distribution: \(f(x, y)\) (Exponential Family)
The joint distribution is:
where:
\(X|Y \sim N(\mu + \gamma Y, \Sigma Y)\)
\(Y \sim \text{GIG}(p, a, b)\)
[2]:
# Define parameters for 1D joint distribution
params_1d = {
'mu': np.array([0.0]),
'gamma': np.array([0.5]),
'sigma': np.array([[1.0]]),
'p': 1.0,
'a': 1.0,
'b': 1.0
}
# Create joint distribution
jgh_1d = JointGeneralizedHyperbolic.from_classical_params(**params_1d)
print("Created:", jgh_1d)
print("\nClassical parameters:", jgh_1d.classical_params)
Created: JointGeneralizedHyperbolic(μ=0.000, γ=0.500, p=1.000, a=1.000, b=1.000)
Classical parameters: GHParams(mu=array([0.]), gamma=array([0.5]), sigma=array([[1.]]), p=np.float64(1.0), a=np.float64(1.0), b=np.float64(1.0))
[3]:
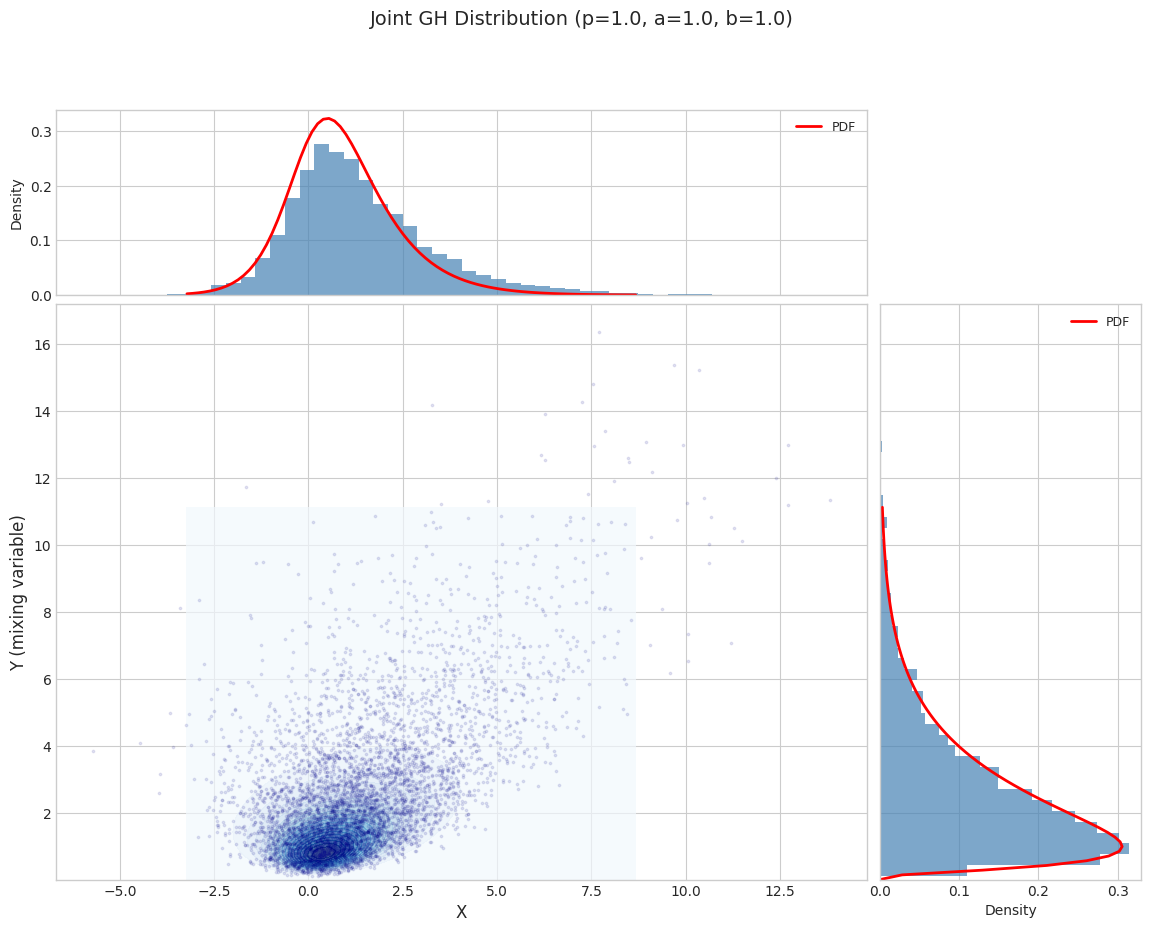
# Visualize joint distribution
fig = plot_joint_distribution_1d(
jgh_1d, n_samples=5000, random_state=42,
title=f"Joint GH Distribution (p={params_1d['p']}, a={params_1d['a']}, b={params_1d['b']})"
)
plt.tight_layout()
plt.show()
/tmp/ipykernel_2346057/2167798511.py:6: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
plt.tight_layout()
1.1 Moment Validation
[4]:
# Validate moments
moment_results = validate_moments(jgh_1d, n_samples=20000, random_state=42, is_joint=True)
print_moment_validation(moment_results)
============================================================
Moment Validation: Distribution
============================================================
X_mean : sample = 1.3374, theory = 1.3497, rel_err = 9.18e-03
Y_mean : sample = 2.7129, theory = 2.6995, rel_err = 4.98e-03
X_var : sample = 3.8364, theory = 3.8272, rel_err = 2.43e-03
Y_var : sample = 4.5105, theory = 4.5107, rel_err = 5.71e-05
1.2 MLE Fitting (Complete Data)
[5]:
# Test MLE fitting for joint distribution
fitted_dist, fitted_params, param_errors = test_joint_fitting(
JointGeneralizedHyperbolic,
params_1d,
n_samples=10000,
random_state=42
)
print_fitting_results(params_1d, fitted_params, param_errors, name="JointGH")
============================================================
Fitting Results: JointGH
============================================================
Parameter True Fitted Rel.Error
------------------------------------------------------------
mu 0.0000 -0.0110 1.10e+08
gamma 0.5000 0.5025 5.00e-03
sigma 1.0000 1.0071 7.11e-03
p 1.0000 0.9702 2.98e-02
a 1.0000 0.9982 1.76e-03
b 1.0000 1.0471 4.71e-02
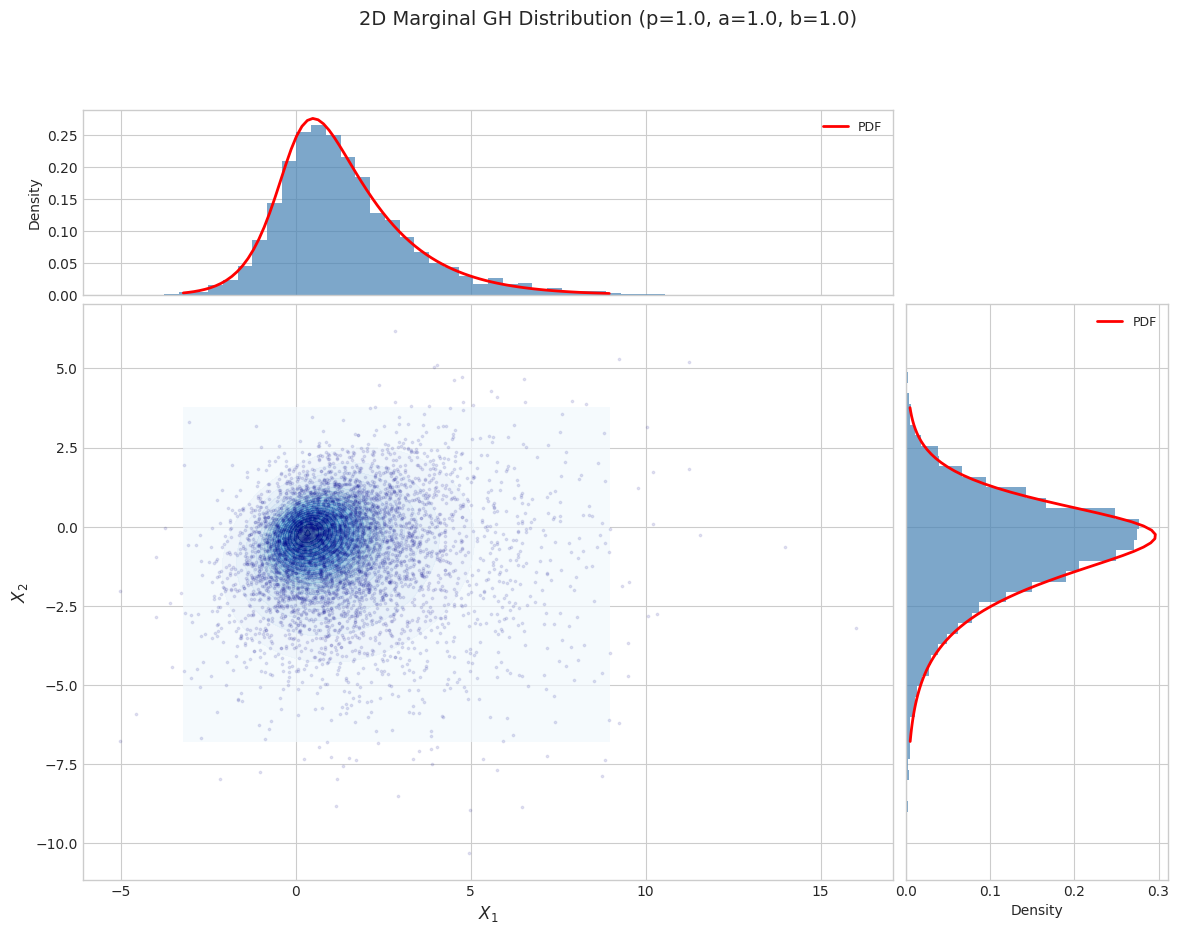
2. Marginal Distribution: \(f(x)\) (2D Case)
The marginal distribution is NOT an exponential family.
[6]:
# Define 2D marginal distribution parameters
params_2d = {
'mu': np.array([0.0, 0.0]),
'gamma': np.array([0.5, -0.3]),
'sigma': np.array([[1.0, 0.3], [0.3, 1.0]]),
'p': 1.0,
'a': 1.0,
'b': 1.0
}
# Create marginal distribution
gh_2d = GeneralizedHyperbolic.from_classical_params(**params_2d)
print("Created:", gh_2d)
Created: GeneralizedHyperbolic(d=2, p=1.000, a=1.000, b=1.000)
[7]:
# Visualize 2D marginal distribution
fig = plot_marginal_distribution_2d(
gh_2d, n_samples=5000, random_state=42,
title=f"2D Marginal GH Distribution (p={params_2d['p']}, a={params_2d['a']}, b={params_2d['b']})"
)
plt.tight_layout()
plt.show()
/tmp/ipykernel_2346057/2887610028.py:6: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
plt.tight_layout()
2.1 EM Algorithm Fitting
The marginal distribution requires the EM algorithm for fitting.
[17]:
# Generate data from true distribution
true_gh = GeneralizedHyperbolic.from_classical_params(**params_2d)
X_data = true_gh.rvs(size=5000, random_state=42)
# Compute true log-likelihood for reference
true_ll = np.mean(true_gh.logpdf(X_data))
print(f"True parameters log-likelihood: {true_ll:.4f}")
# Fit using EM algorithm with regularization
print("\nFitting with EM algorithm (det_sigma_one regularization)...")
fitted_gh, convergence = fit_and_track_convergence(
GeneralizedHyperbolic,
X_data,
max_iter=100,
tol=1e-2, # Use reasonable tolerance for GH
regularization='det_sigma_one',
)
print(f"\nConverged: {convergence.converged}")
print(f"Final log-likelihood: {convergence.log_likelihoods[-1]:.4f}")
print(f"Improvement over true: {convergence.log_likelihoods[-1] - true_ll:.4f}")
True parameters log-likelihood: -3.8839
Fitting with EM algorithm (det_sigma_one regularization)...
Converged: True
Final log-likelihood: -3.8824
Improvement over true: 0.0015
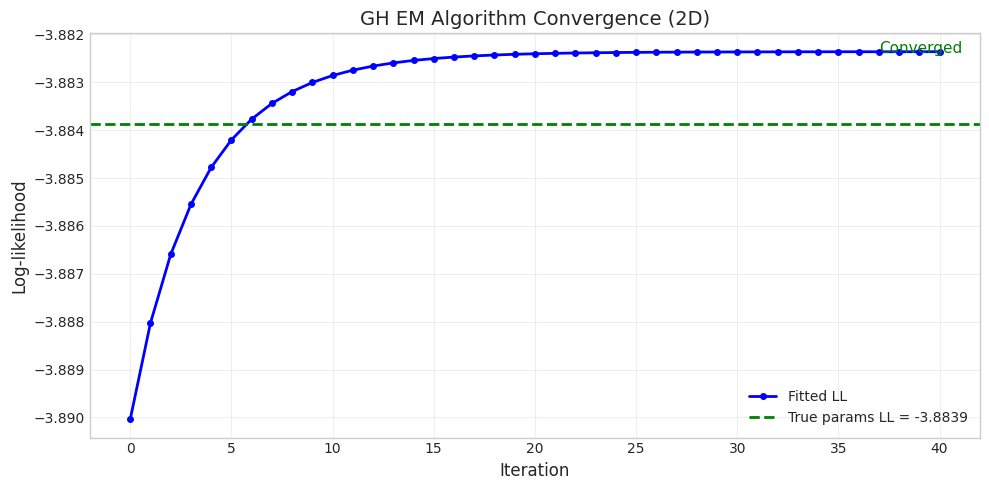
[18]:
# Plot convergence with true log-likelihood reference
fig = plot_em_convergence(
convergence,
title="GH EM Algorithm Convergence (2D)",
true_ll=true_ll
)
plt.show()
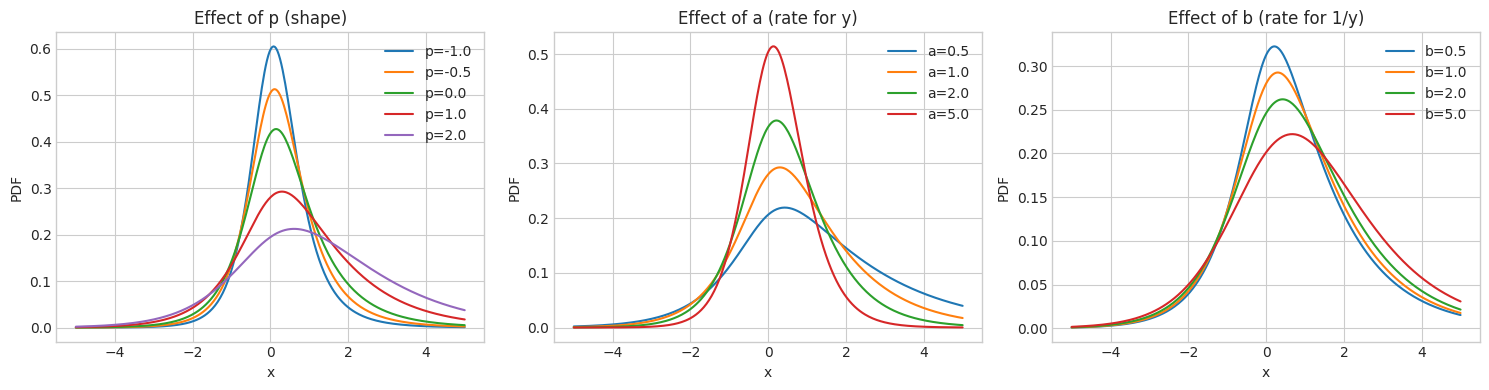
3. Effect of GIG Parameters
The GIG parameters \((p, a, b)\) control the shape of the mixing distribution and thus the behavior of the GH distribution.
[10]:
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# Base parameters
base_mu = np.array([0.0])
base_gamma = np.array([0.3])
base_sigma = np.array([[1.0]])
x = np.linspace(-5, 5, 300)
# Effect of p
ax = axes[0]
for p in [-1.0, -0.5, 0.0, 1.0, 2.0]:
try:
gh = GeneralizedHyperbolic.from_classical_params(
mu=base_mu, gamma=base_gamma, sigma=base_sigma, p=p, a=1.0, b=1.0
)
pdf = np.array([gh.pdf(np.array([xi])) for xi in x])
ax.plot(x, pdf, label=f'p={p}')
except:
pass
ax.set_title('Effect of p (shape)')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
ax.legend()
# Effect of a
ax = axes[1]
for a in [0.5, 1.0, 2.0, 5.0]:
try:
gh = GeneralizedHyperbolic.from_classical_params(
mu=base_mu, gamma=base_gamma, sigma=base_sigma, p=1.0, a=a, b=1.0
)
pdf = np.array([gh.pdf(np.array([xi])) for xi in x])
ax.plot(x, pdf, label=f'a={a}')
except:
pass
ax.set_title('Effect of a (rate for y)')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
ax.legend()
# Effect of b
ax = axes[2]
for b in [0.5, 1.0, 2.0, 5.0]:
try:
gh = GeneralizedHyperbolic.from_classical_params(
mu=base_mu, gamma=base_gamma, sigma=base_sigma, p=1.0, a=1.0, b=b
)
pdf = np.array([gh.pdf(np.array([xi])) for xi in x])
ax.plot(x, pdf, label=f'b={b}')
except:
pass
ax.set_title('Effect of b (rate for 1/y)')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
ax.legend()
plt.tight_layout()
plt.show()
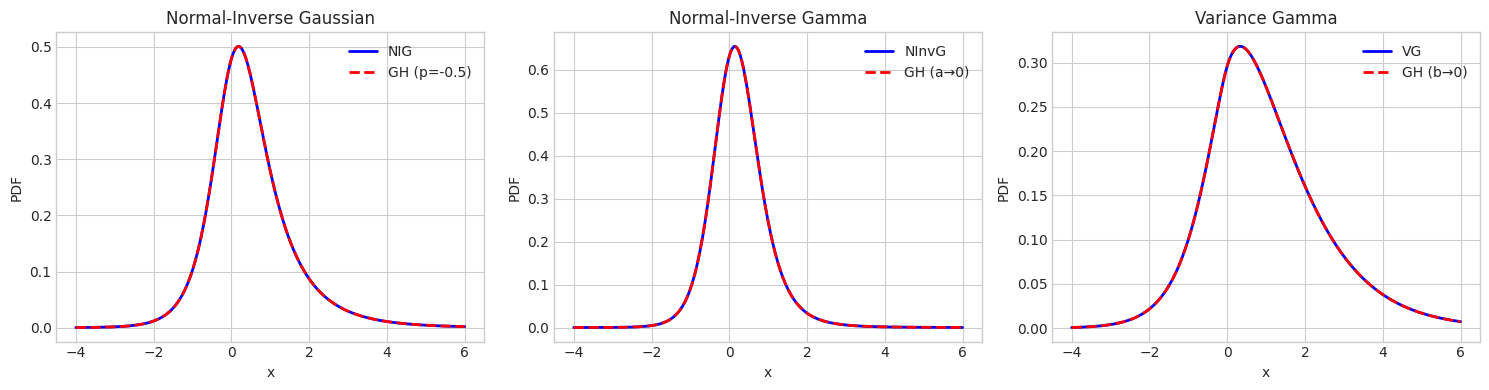
4. Special Case Comparison
Verify that GH special cases match their dedicated implementations.
[11]:
# Test parameters
mu = np.array([0.0])
gamma = np.array([0.5])
sigma = np.array([[1.0]])
x = np.linspace(-4, 6, 300)
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# NIG comparison (p = -0.5)
ax = axes[0]
nig_params = {'delta': 1.0, 'eta': 1.0}
nig = NormalInverseGaussian.from_classical_params(mu=mu, gamma=gamma, sigma=sigma, **nig_params)
gh_nig = GeneralizedHyperbolic.as_normal_inverse_gaussian(mu=mu, gamma=gamma, sigma=sigma, **nig_params)
nig_pdf = np.array([nig.pdf(np.array([xi])) for xi in x])
gh_nig_pdf = np.array([gh_nig.pdf(np.array([xi])) for xi in x])
ax.plot(x, nig_pdf, 'b-', linewidth=2, label='NIG')
ax.plot(x, gh_nig_pdf, 'r--', linewidth=2, label='GH (p=-0.5)')
ax.set_title('Normal-Inverse Gaussian')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
ax.legend()
print(f"NIG mean: {nig.mean()}, GH mean: {gh_nig.mean()}")
# NInvG comparison (a → 0)
ax = axes[1]
ninvg_params = {'shape': 3.0, 'rate': 1.0}
ninvg = NormalInverseGamma.from_classical_params(mu=mu, gamma=gamma, sigma=sigma, **ninvg_params)
gh_ninvg = GeneralizedHyperbolic.as_normal_inverse_gamma(mu=mu, gamma=gamma, sigma=sigma, **ninvg_params)
ninvg_pdf = np.array([ninvg.pdf(np.array([xi])) for xi in x])
gh_ninvg_pdf = np.array([gh_ninvg.pdf(np.array([xi])) for xi in x])
ax.plot(x, ninvg_pdf, 'b-', linewidth=2, label='NInvG')
ax.plot(x, gh_ninvg_pdf, 'r--', linewidth=2, label='GH (a→0)')
ax.set_title('Normal-Inverse Gamma')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
ax.legend()
print(f"NInvG mean: {ninvg.mean()}, GH mean: {gh_ninvg.mean()}")
# VG comparison (b → 0)
ax = axes[2]
vg_params = {'shape': 2.0, 'rate': 1.0}
vg = VarianceGamma.from_classical_params(mu=mu, gamma=gamma, sigma=sigma, **vg_params)
gh_vg = GeneralizedHyperbolic.as_variance_gamma(mu=mu, gamma=gamma, sigma=sigma, **vg_params)
vg_pdf = np.array([vg.pdf(np.array([xi])) for xi in x])
gh_vg_pdf = np.array([gh_vg.pdf(np.array([xi])) for xi in x])
ax.plot(x, vg_pdf, 'b-', linewidth=2, label='VG')
ax.plot(x, gh_vg_pdf, 'r--', linewidth=2, label='GH (b→0)')
ax.set_title('Variance Gamma')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
ax.legend()
print(f"VG mean: {vg.mean()}, GH mean: {gh_vg.mean()}")
plt.tight_layout()
plt.show()
NIG mean: [0.5], GH mean: [0.5]
NInvG mean: [0.25], GH mean: [0.25]
VG mean: [1.], GH mean: [1.]
5. Parameter Regularization
The GH model is not identifiable since \((\mu, \gamma/c, \Sigma/c, p, cb, a/c)\) gives the same distribution for any \(c > 0\).
Available regularization methods:
det_sigma_one: Fix \(|\Sigma| = 1\) (recommended)sigma_diagonal_one: Fix \(\Sigma_{11} = 1\)fix_p: Fix \(p\) to a specific valuenone: No regularization
[12]:
from normix.distributions.mixtures import REGULARIZATION_METHODS
print("Available regularization methods:")
for name in REGULARIZATION_METHODS:
print(f" - {name}")
Available regularization methods:
- det_sigma_one
- sigma_diagonal_one
- fix_p
- none
[13]:
# Compare different regularizations
X_data = true_gh.rvs(size=3000, random_state=42)
regularizations = ['det_sigma_one', 'fix_p']
results = {}
for reg in regularizations:
print(f"\n--- Regularization: {reg} ---")
fitted = GeneralizedHyperbolic()
kwargs = {'regularization': reg}
if reg == 'fix_p':
kwargs['regularization_params'] = {'p_fixed': 1.0}
fitted.fit(X_data, max_iter=30, verbose=0, **kwargs)
params = fitted.classical_params
print(f" p = {params.p:.4f}")
print(f" a = {params.a:.4f}")
print(f" b = {params.b:.4f}")
print(f" |Σ| = {np.linalg.det(params.sigma):.4f}")
print(f" Mean = {fitted.mean()}")
results[reg] = fitted
--- Regularization: det_sigma_one ---
p = 0.5896
a = 0.9347
b = 1.6064
|Σ| = 1.0000
Mean = [ 1.27654667 -0.82581383]
--- Regularization: fix_p ---
p = 1.0000
a = 0.3575
b = 14.3831
|Σ| = 0.0738
Mean = [ 1.58034717 -1.01797886]
6. Exponential Family Structure
The joint distribution is an exponential family with:
Sufficient statistics:
Natural parameters:
[15]:
# Show parameter conversions
print("=== Exponential Family Parameters ===")
print(f"\nClassical: {jgh_1d.classical_params}")
print(f"\nNatural: {jgh_1d.natural_params}")
print(f"\nExpectation: {jgh_1d.expectation_params[:6]}...") # First 6 components
=== Exponential Family Parameters ===
Classical: GHParams(mu=array([0.]), gamma=array([0.5]), sigma=array([[1.]]), p=np.float64(1.0), a=np.float64(1.0), b=np.float64(1.0))
Natural: [-0.5 -1. -1.125 0.5 0. -0.5 ]
Expectation: [0.69948394 0.69948394 2.69948394 1.34974197 0.5 1.67487098]...
[16]:
# Verify sufficient statistics match expectation parameters
n_samples = 20000
X, Y = jgh_1d.rvs(size=n_samples, random_state=42)
t_samples = jgh_1d._sufficient_statistics(X, Y)
eta_sample = np.mean(t_samples, axis=0)
eta_theory = jgh_1d.expectation_params
print("E[t(X,Y)] from samples vs theoretical:")
print(f" E[log Y]: {eta_sample[0]:.4f} vs {eta_theory[0]:.4f}")
print(f" E[1/Y]: {eta_sample[1]:.4f} vs {eta_theory[1]:.4f}")
print(f" E[Y]: {eta_sample[2]:.4f} vs {eta_theory[2]:.4f}")
E[t(X,Y)] from samples vs theoretical:
E[log Y]: 0.7052 vs 0.6995
E[1/Y]: 0.6942 vs 0.6995
E[Y]: 2.7129 vs 2.6995
Summary
The Generalized Hyperbolic distribution:
Most general normal variance-mean mixture
Joint distribution is an exponential family
Marginal distribution requires EM algorithm for fitting
Special cases include VG, NIG, NInvG, and more
Regularization is needed due to identifiability issues