This page was generated from a Jupyter notebook. You can view it on GitHub or download and run it locally.
S&P 500 Stocks Multivariate Empirical Study
This notebook compares multivariate probability distributions for modeling S&P 500 stock returns. The main purpose is to test the EM algorithm in real-world high-dimensional settings.
Distributions Compared
Multivariate Normal - Baseline Gaussian distribution
Variance Gamma (VG) - Normal-Gamma mixture, semi-heavy tails
Normal Inverse Gamma (NInvG) - Normal-InverseGamma mixture, heavy tails
Normal Inverse Gaussian (NIG) - Normal-InverseGaussian mixture
Generalized Hyperbolic (GH) - Most general, encompasses VG, NInvG, NIG as special cases
Methodology
Data: 10 years of S&P 500 constituent stocks daily returns
Training: First 5 years (in-sample)
Testing: Last 5 years (out-of-sample)
EM Algorithm: Track convergence and timing in high dimensions
Testing Methods: Random portfolio projections, KS/AD tests, QQ plots
Parameter Analysis: Compare location (μ) vs skewness (γ) parameters across stocks
[1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from scipy import stats
from scipy.stats import ks_2samp, anderson_ksamp
import warnings
import time
warnings.filterwarnings('ignore')
# Import normix distributions
from normix.distributions.multivariate import MultivariateNormal
from normix.distributions.mixtures import (
VarianceGamma, NormalInverseGamma, NormalInverseGaussian, GeneralizedHyperbolic
)
plt.style.use('seaborn-v0_8-whitegrid')
%matplotlib inline
print("Imports successful!")
Imports successful!
1. Load S&P 500 Stock Returns Data
The log returns data is pre-computed and stored in data/sp500_returns.csv. This file is generated by scripts/download_sp500_data.py which fetches S&P 500 constituent stocks from Wikipedia and downloads historical price data from Yahoo Finance.
[2]:
# Load pre-computed log returns from CSV
import os
data_path = '../data/sp500_returns.csv'
if not os.path.exists(data_path):
raise FileNotFoundError(
f"Data file not found at {data_path}. "
"Please run 'python scripts/download_sp500_data.py' first to generate the data."
)
log_returns = pd.read_csv(data_path, index_col='Date', parse_dates=True)
print(f"Loaded log returns from: {data_path}")
print(f"Shape: {log_returns.shape}")
print(f"Date range: {log_returns.index[0].date()} to {log_returns.index[-1].date()}")
print(f"Number of stocks: {len(log_returns.columns)}")
print(f"First 10 tickers: {list(log_returns.columns[:10])}")
Loaded log returns from: ../data/sp500_returns.csv
Shape: (2551, 224)
Date range: 2015-12-10 to 2026-02-03
Number of stocks: 224
First 10 tickers: ['A', 'AAPL', 'ABBV', 'ABT', 'ACN', 'ADBE', 'ADI', 'AEP', 'AES', 'AIG']
[3]:
# Use ALL stocks from the CSV file (no filtering needed - data is already clean)
# Note: High-dimensional fitting can be slow - adjust MAX_STOCKS if needed for computational constraints
MAX_STOCKS = None # Set to a number (e.g., 100) to limit, or None for all available stocks
# Select all stocks, sorted alphabetically
all_tickers = sorted(log_returns.columns.tolist())
if MAX_STOCKS is not None and MAX_STOCKS < len(all_tickers):
selected_tickers = all_tickers[:MAX_STOCKS]
print(f"Limited to {MAX_STOCKS} stocks for computational efficiency")
else:
selected_tickers = all_tickers
log_returns_selected = log_returns[selected_tickers]
print(f"Selected {len(selected_tickers)} stocks for analysis:")
print(f"Tickers: {selected_tickers[:20]}{'...' if len(selected_tickers) > 20 else ''}")
Selected 224 stocks for analysis:
Tickers: ['A', 'AAPL', 'ABBV', 'ABT', 'ACN', 'ADBE', 'ADI', 'AEP', 'AES', 'AIG', 'ALL', 'AMAT', 'AMD', 'AMGN', 'AMT', 'AMZN', 'APA', 'APD', 'ARE', 'AVB']...
[4]:
# Split into training (first half) and testing (second half)
n_total = len(log_returns_selected)
n_train = n_total // 2
train_df = log_returns_selected.iloc[:n_train]
test_df = log_returns_selected.iloc[n_train:]
# Convert to numpy arrays
returns_train = train_df.values
returns_test = test_df.values
print(f"\nTraining period: {train_df.index[0].date()} to {train_df.index[-1].date()}")
print(f"Training samples: {returns_train.shape[0]}, dimensions: {returns_train.shape[1]}")
print(f"\nTesting period: {test_df.index[0].date()} to {test_df.index[-1].date()}")
print(f"Testing samples: {returns_test.shape[0]}, dimensions: {returns_test.shape[1]}")
Training period: 2015-12-10 to 2021-01-04
Training samples: 1275, dimensions: 224
Testing period: 2021-01-05 to 2026-02-03
Testing samples: 1276, dimensions: 224
[5]:
# Display training data statistics
print("--- Training Data Statistics ---")
mean_returns = returns_train.mean(axis=0) * 100
std_returns = returns_train.std(axis=0) * 100
skewness = stats.skew(returns_train, axis=0)
kurtosis = stats.kurtosis(returns_train, axis=0)
stats_df = pd.DataFrame({
'Mean (%)': mean_returns,
'Std (%)': std_returns,
'Skewness': skewness,
'Kurtosis': kurtosis
}, index=selected_tickers)
print(stats_df.round(4))
print(f"\n--- Summary ---")
print(f"Average mean return: {mean_returns.mean():.4f}%")
print(f"Average volatility: {std_returns.mean():.4f}%")
print(f"Average skewness: {skewness.mean():.4f}")
print(f"Average excess kurtosis: {kurtosis.mean():.4f}")
--- Training Data Statistics ---
Mean (%) Std (%) Skewness Kurtosis
A 0.0872 1.6669 -0.6919 7.1136
AAPL 0.1236 1.8991 -0.3552 7.4072
ABBV 0.0669 1.8452 -1.0039 14.5807
ABT 0.0772 1.5974 -0.3903 7.7395
ACN 0.0751 1.5903 -0.0063 8.8244
... ... ... ... ...
WMB -0.0040 3.1997 -1.8227 39.9337
WMT 0.0801 1.3877 0.7979 15.6157
XEL 0.0612 1.4044 -1.0123 19.8592
XOM -0.0285 1.8035 -0.1616 10.5633
ZBH 0.0368 1.8834 -0.1455 12.3800
[224 rows x 4 columns]
--- Summary ---
Average mean return: 0.0523%
Average volatility: 1.9748%
Average skewness: -0.5328
Average excess kurtosis: 17.8969
2. Fit Distributions with EM Algorithm Tracking
[6]:
# Storage for fitted distributions and convergence info
fitted_dists = {}
fitting_times = {}
convergence_history = {}
d = returns_train.shape[1] # dimension
print(f"Fitting distributions to {d}-dimensional data...")
Fitting distributions to 224-dimensional data...
2.1 Multivariate Normal (Baseline)
[7]:
print("Fitting Multivariate Normal...")
start_time = time.time()
mvn = MultivariateNormal(d=d).fit(returns_train)
fitting_times['MVN'] = time.time() - start_time
fitted_dists['MVN'] = mvn
print(f"Fitting time: {fitting_times['MVN']:.2f}s")
print(f"Mean log-likelihood (train): {np.mean(mvn.logpdf(returns_train)):.4f}")
print(f"Mean log-likelihood (test): {np.mean(mvn.logpdf(returns_test)):.4f}")
Fitting Multivariate Normal...
Fitting time: 0.08s
Mean log-likelihood (train): 702.2173
Mean log-likelihood (test): 624.0910
2.2 Variance Gamma (VG)
[8]:
print("Fitting Variance Gamma...")
start_time = time.time()
# Create a custom verbose fit to track convergence
vg = VarianceGamma()
vg_ll_history = []
# We'll manually track convergence by fitting with verbose=2
# and capturing the output, or by modifying the fit loop
# For simplicity, just fit with verbose
vg.fit(returns_train, max_iter=100, tol=1e-3, verbose=1)
fitting_times['VG'] = time.time() - start_time
fitted_dists['VG'] = vg
print(f"\nFitting time: {fitting_times['VG']:.2f}s")
print(f"Mean log-likelihood (train): {np.mean(vg.logpdf(returns_train)):.4f}")
print(f"Mean log-likelihood (test): {np.mean(vg.logpdf(returns_test)):.4f}")
Fitting Variance Gamma...
Initial log-likelihood: 445.622318
Iteration 1: log-likelihood = 702.301546
Iteration 2: log-likelihood = 712.297042
Iteration 3: log-likelihood = 718.818670
Iteration 4: log-likelihood = 720.217824
Iteration 5: log-likelihood = 720.394836
Iteration 6: log-likelihood = 720.414506
Iteration 7: log-likelihood = 720.416618
Iteration 8: log-likelihood = 720.416843
Iteration 9: log-likelihood = 720.416867
Iteration 10: log-likelihood = 720.416869
Converged at iteration 10
Final log-likelihood: 720.416869
Fitting time: 2.68s
Mean log-likelihood (train): 720.4169
Mean log-likelihood (test): 666.1294
2.3 Normal Inverse Gamma (NInvG)
[9]:
print("Fitting Normal Inverse Gamma...")
start_time = time.time()
ninvg = NormalInverseGamma()
ninvg.fit(returns_train, max_iter=100, tol=1e-3, verbose=1)
fitting_times['NInvG'] = time.time() - start_time
fitted_dists['NInvG'] = ninvg
print(f"\nFitting time: {fitting_times['NInvG']:.2f}s")
print(f"Mean log-likelihood (train): {np.mean(ninvg.logpdf(returns_train)):.4f}")
print(f"Mean log-likelihood (test): {np.mean(ninvg.logpdf(returns_test)):.4f}")
Fitting Normal Inverse Gamma...
Initial log-likelihood: 667.849344
Iteration 1: log-likelihood = 714.870073
Iteration 2: log-likelihood = 720.056497
Iteration 3: log-likelihood = 720.590019
Iteration 4: log-likelihood = 720.629384
Iteration 5: log-likelihood = 720.632118
Iteration 6: log-likelihood = 720.632313
Iteration 7: log-likelihood = 720.632327
Iteration 8: log-likelihood = 720.632328
Converged at iteration 8
Final log-likelihood: 720.632328
Fitting time: 0.21s
Mean log-likelihood (train): 720.6323
Mean log-likelihood (test): 666.0525
2.4 Normal Inverse Gaussian (NIG)
[10]:
print("Fitting Normal Inverse Gaussian...")
start_time = time.time()
nig = NormalInverseGaussian()
nig.fit(returns_train, max_iter=100, tol=1e-3, verbose=1)
fitting_times['NIG'] = time.time() - start_time
fitted_dists['NIG'] = nig
print(f"\nFitting time: {fitting_times['NIG']:.2f}s")
print(f"Mean log-likelihood (train): {np.mean(nig.logpdf(returns_train)):.4f}")
print(f"Mean log-likelihood (test): {np.mean(nig.logpdf(returns_test)):.4f}")
Fitting Normal Inverse Gaussian...
Initial log-likelihood: 529.719043
Iteration 1: log-likelihood = 706.340524
Iteration 2: log-likelihood = 718.128162
Iteration 3: log-likelihood = 720.312762
Iteration 4: log-likelihood = 720.540481
Iteration 5: log-likelihood = 720.560807
Iteration 6: log-likelihood = 720.562597
Iteration 7: log-likelihood = 720.562757
Iteration 8: log-likelihood = 720.562771
Iteration 9: log-likelihood = 720.562772
Converged at iteration 9
Final log-likelihood: 720.562772
Fitting time: 2.48s
Mean log-likelihood (train): 720.5628
Mean log-likelihood (test): 666.1407
2.5 Generalized Hyperbolic (GH)
[11]:
print("Fitting Generalized Hyperbolic...")
print("This is the most general model and may take longer...")
start_time = time.time()
gh = GeneralizedHyperbolic()
gh.fit(returns_train, max_iter=100, tol=1e-3, verbose=1, regularization='det_sigma_one')
fitting_times['GH'] = time.time() - start_time
fitted_dists['GH'] = gh
print(f"\nFitting time: {fitting_times['GH']:.2f}s")
print(f"Mean log-likelihood (train): {np.mean(gh.logpdf(returns_train)):.4f}")
print(f"Mean log-likelihood (test): {np.mean(gh.logpdf(returns_test)):.4f}")
Fitting Generalized Hyperbolic...
This is the most general model and may take longer...
Initial log-likelihood: 720.560807
Iteration 1: log-likelihood = 720.562228
Iteration 2: log-likelihood = 720.562318
Iteration 3: log-likelihood = 720.562324
Iteration 4: log-likelihood = 720.562325
Converged
Fitting time: 3.60s
Mean log-likelihood (train): 720.5623
Mean log-likelihood (test): 666.1362
3. Summary of Fitting Results
[12]:
# Compute log-likelihoods for all distributions
results = []
for name, dist in fitted_dists.items():
train_ll = np.mean(dist.logpdf(returns_train))
test_ll = np.mean(dist.logpdf(returns_test))
results.append({
'Distribution': name,
'Train LL': train_ll,
'Test LL': test_ll,
'Fitting Time (s)': fitting_times[name]
})
results_df = pd.DataFrame(results)
results_df = results_df.sort_values('Test LL', ascending=False)
print("\n" + "="*70)
print("SUMMARY: Distribution Fitting Results")
print("="*70)
print(results_df.to_string(index=False))
print("="*70)
======================================================================
SUMMARY: Distribution Fitting Results
======================================================================
Distribution Train LL Test LL Fitting Time (s)
NIG 720.562772 666.140655 2.481778
GH 720.562325 666.136179 3.599135
VG 720.416869 666.129448 2.676722
NInvG 720.632328 666.052491 0.207242
MVN 702.217252 624.090997 0.076318
======================================================================
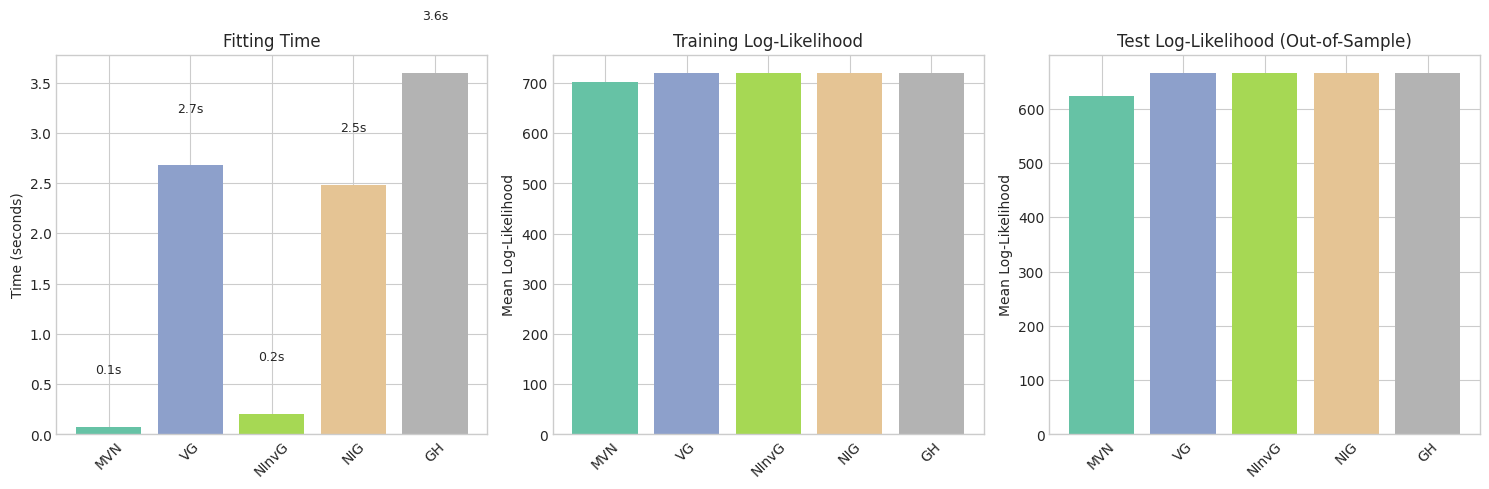
[13]:
# Visualization of fitting times and log-likelihoods
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
dist_names = list(fitted_dists.keys())
colors = plt.cm.Set2(np.linspace(0, 1, len(dist_names)))
# Plot 1: Fitting times
ax1 = axes[0]
times = [fitting_times[n] for n in dist_names]
bars1 = ax1.bar(dist_names, times, color=colors)
ax1.set_ylabel('Time (seconds)')
ax1.set_title('Fitting Time')
ax1.tick_params(axis='x', rotation=45)
# Add value labels
for bar, t in zip(bars1, times):
ax1.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.5,
f'{t:.1f}s', ha='center', va='bottom', fontsize=9)
# Plot 2: Train log-likelihood
ax2 = axes[1]
train_lls = [np.mean(fitted_dists[n].logpdf(returns_train)) for n in dist_names]
bars2 = ax2.bar(dist_names, train_lls, color=colors)
ax2.set_ylabel('Mean Log-Likelihood')
ax2.set_title('Training Log-Likelihood')
ax2.tick_params(axis='x', rotation=45)
# Plot 3: Test log-likelihood
ax3 = axes[2]
test_lls = [np.mean(fitted_dists[n].logpdf(returns_test)) for n in dist_names]
bars3 = ax3.bar(dist_names, test_lls, color=colors)
ax3.set_ylabel('Mean Log-Likelihood')
ax3.set_title('Test Log-Likelihood (Out-of-Sample)')
ax3.tick_params(axis='x', rotation=45)
plt.tight_layout()
plt.savefig('fitting_summary.png', dpi=150, bbox_inches='tight')
plt.show()
4. Random Portfolio Projections Testing
To test multivariate distributions, we use random portfolio projections:
Generate random weight vectors
Project returns onto 1D using these weights
Compare simulated samples from fitted distributions vs actual test data
Use KS and Anderson-Darling tests
[14]:
def generate_random_weights(d, n_portfolios=100, random_state=None):
"""
Generate random portfolio weights.
Parameters
----------
d : int
Number of assets.
n_portfolios : int
Number of random portfolios to generate.
random_state : int, optional
Random seed.
Returns
-------
weights : ndarray
Shape (n_portfolios, d), each row sums to 1.
"""
rng = np.random.default_rng(random_state)
# Generate random weights from Dirichlet distribution (uniform on simplex)
# This ensures weights are positive and sum to 1
weights = rng.dirichlet(np.ones(d), size=n_portfolios)
return weights
def project_returns(returns, weights):
"""
Project multivariate returns to 1D portfolio returns.
Parameters
----------
returns : ndarray
Shape (n_samples, d).
weights : ndarray
Shape (n_portfolios, d) or (d,).
Returns
-------
portfolio_returns : ndarray
Shape (n_samples, n_portfolios) or (n_samples,).
"""
if weights.ndim == 1:
return returns @ weights
else:
return returns @ weights.T
[15]:
# Generate random portfolios
N_PORTFOLIOS = 100
random_weights = generate_random_weights(d, n_portfolios=N_PORTFOLIOS, random_state=42)
print(f"Generated {N_PORTFOLIOS} random portfolios")
print(f"Weight matrix shape: {random_weights.shape}")
print(f"First portfolio weights: {random_weights[0][:5].round(3)}...")
Generated 100 random portfolios
Weight matrix shape: (100, 224)
First portfolio weights: [0.011 0.011 0.011 0.001 0. ]...
[16]:
def portfolio_test(dist, returns_test, weights, n_samples=10000, random_state=None):
"""
Test a distribution using random portfolio projections.
Parameters
----------
dist : distribution object
Fitted distribution.
returns_test : ndarray
Test data, shape (n_test, d).
weights : ndarray
Portfolio weights, shape (n_portfolios, d).
n_samples : int
Number of samples to generate from distribution.
random_state : int, optional
Random seed.
Returns
-------
results : dict
Dictionary with KS and AD test statistics.
"""
# Generate samples from fitted distribution
samples = dist.rvs(size=n_samples, random_state=random_state)
n_portfolios = weights.shape[0]
ks_stats = []
ks_pvals = []
ad_stats = []
for i in range(n_portfolios):
w = weights[i]
# Project to 1D
test_proj = returns_test @ w
sample_proj = samples @ w
# KS test
ks_stat, ks_pval = ks_2samp(test_proj, sample_proj)
ks_stats.append(ks_stat)
ks_pvals.append(ks_pval)
# Anderson-Darling test (two-sample)
try:
ad_result = anderson_ksamp([test_proj, sample_proj])
ad_stats.append(ad_result.statistic)
except Exception:
ad_stats.append(np.nan)
return {
'ks_stats': np.array(ks_stats),
'ks_pvals': np.array(ks_pvals),
'ad_stats': np.array(ad_stats),
'ks_mean': np.mean(ks_stats),
'ks_median': np.median(ks_stats),
'ad_mean': np.nanmean(ad_stats),
'ad_median': np.nanmedian(ad_stats),
'ks_reject_rate': np.mean(np.array(ks_pvals) < 0.05) # Rejection rate at 5%
}
[17]:
# Run portfolio tests for all distributions
portfolio_results = {}
print("Running portfolio projection tests...")
print(f"Testing with {N_PORTFOLIOS} random portfolios\n")
for name, dist in fitted_dists.items():
print(f"Testing {name}...")
try:
results = portfolio_test(dist, returns_test, random_weights,
n_samples=5000, random_state=42)
portfolio_results[name] = results
print(f" KS mean: {results['ks_mean']:.4f}, KS reject rate: {results['ks_reject_rate']:.2%}")
print(f" AD mean: {results['ad_mean']:.4f}")
except Exception as e:
print(f" Error: {e}")
portfolio_results[name] = None
Running portfolio projection tests...
Testing with 100 random portfolios
Testing MVN...
KS mean: 0.1124, KS reject rate: 100.00%
AD mean: 41.9969
Testing VG...
KS mean: 0.0384, KS reject rate: 15.00%
AD mean: 3.4969
Testing NInvG...
KS mean: 0.0328, KS reject rate: 1.00%
AD mean: 0.8984
Testing NIG...
KS mean: 0.0360, KS reject rate: 10.00%
AD mean: 1.5887
Testing GH...
KS mean: 0.0374, KS reject rate: 19.00%
AD mean: 1.8635
[18]:
# Summary of portfolio tests
test_summary = []
for name, results in portfolio_results.items():
if results is not None:
test_summary.append({
'Distribution': name,
'KS Mean': results['ks_mean'],
'KS Median': results['ks_median'],
'KS Reject Rate': results['ks_reject_rate'],
'AD Mean': results['ad_mean'],
'AD Median': results['ad_median']
})
test_df = pd.DataFrame(test_summary)
test_df = test_df.sort_values('KS Mean')
print("\n" + "="*80)
print("PORTFOLIO PROJECTION TEST RESULTS")
print("Lower KS/AD statistics indicate better fit")
print("="*80)
print(test_df.to_string(index=False))
print("="*80)
================================================================================
PORTFOLIO PROJECTION TEST RESULTS
Lower KS/AD statistics indicate better fit
================================================================================
Distribution KS Mean KS Median KS Reject Rate AD Mean AD Median
NInvG 0.032845 0.032740 0.01 0.898434 0.797889
NIG 0.035985 0.037087 0.10 1.588689 1.574836
GH 0.037391 0.037722 0.19 1.863452 1.757622
VG 0.038414 0.038188 0.15 3.496930 3.348221
MVN 0.112396 0.112363 1.00 41.996915 41.885030
================================================================================
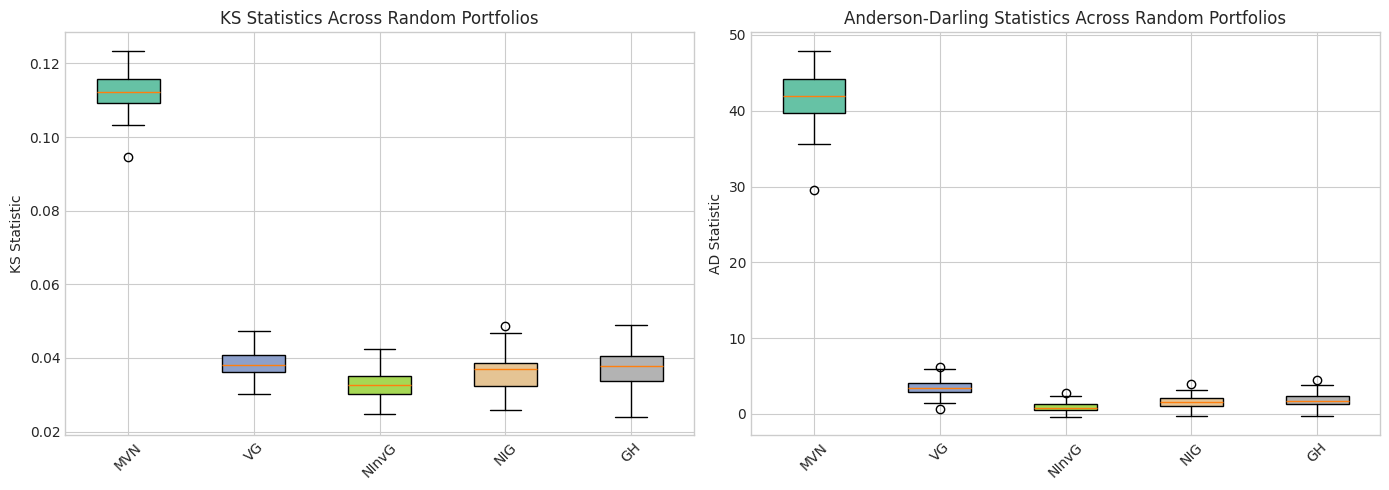
[19]:
# Visualize test statistics distribution
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
# KS statistics boxplot
ax1 = axes[0]
ks_data = [portfolio_results[n]['ks_stats'] for n in fitted_dists.keys() if portfolio_results[n] is not None]
ks_labels = [n for n in fitted_dists.keys() if portfolio_results[n] is not None]
bp1 = ax1.boxplot(ks_data, labels=ks_labels, patch_artist=True)
for patch, color in zip(bp1['boxes'], colors[:len(ks_labels)]):
patch.set_facecolor(color)
ax1.set_ylabel('KS Statistic')
ax1.set_title('KS Statistics Across Random Portfolios')
ax1.tick_params(axis='x', rotation=45)
# AD statistics boxplot
ax2 = axes[1]
ad_data = [portfolio_results[n]['ad_stats'] for n in fitted_dists.keys() if portfolio_results[n] is not None]
ad_labels = [n for n in fitted_dists.keys() if portfolio_results[n] is not None]
bp2 = ax2.boxplot(ad_data, labels=ad_labels, patch_artist=True)
for patch, color in zip(bp2['boxes'], colors[:len(ad_labels)]):
patch.set_facecolor(color)
ax2.set_ylabel('AD Statistic')
ax2.set_title('Anderson-Darling Statistics Across Random Portfolios')
ax2.tick_params(axis='x', rotation=45)
plt.tight_layout()
plt.savefig('portfolio_test_boxplots.png', dpi=150, bbox_inches='tight')
plt.show()
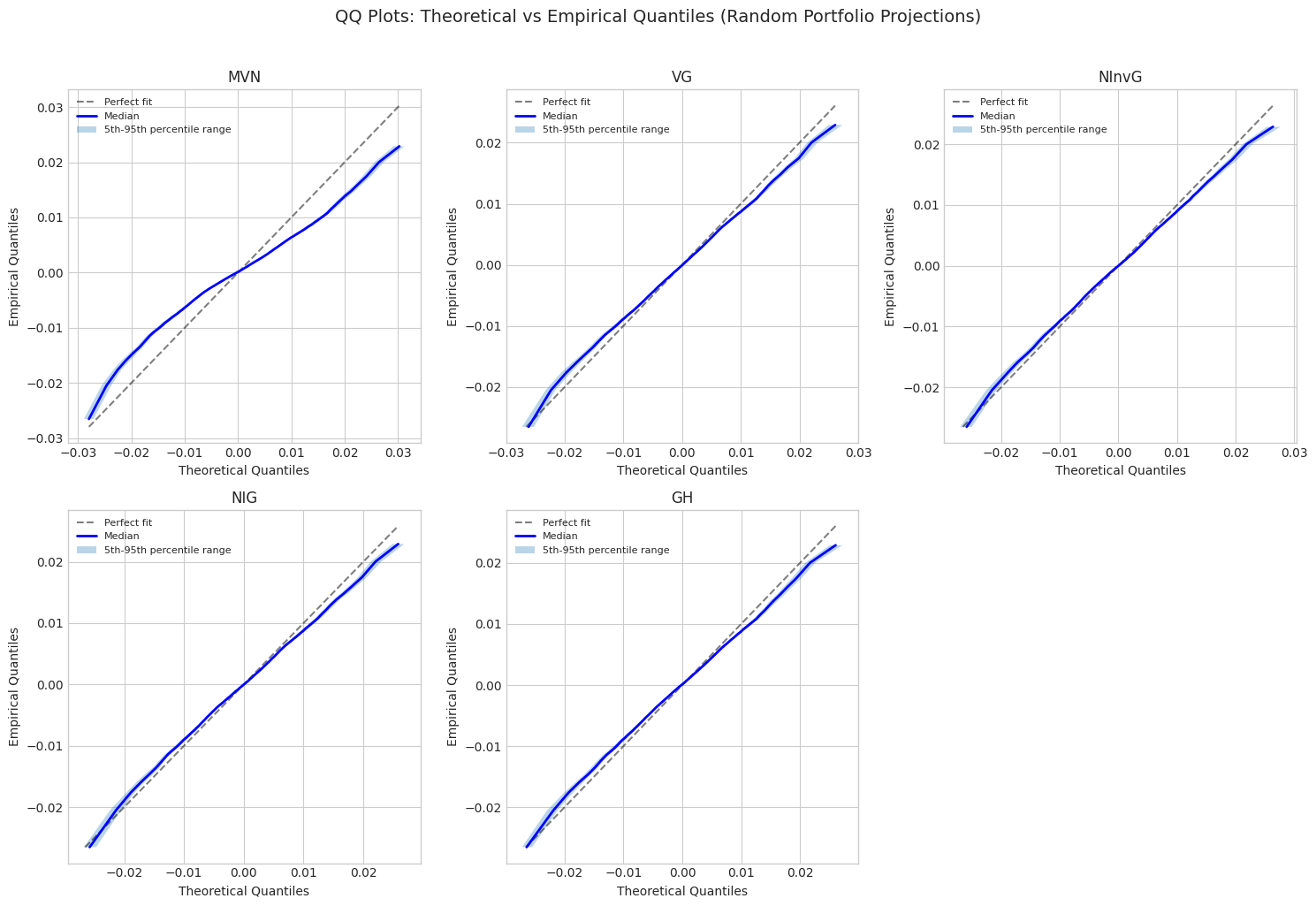
5. Quantile Range Plots
For each random portfolio, compare quantiles of simulated vs actual data.
[20]:
def compute_quantile_comparison(dist, returns_test, weights,
quantiles=np.linspace(0.01, 0.99, 99),
n_samples=10000, random_state=None):
"""
Compute quantile comparison for multiple portfolios.
Returns arrays of (empirical quantiles, theoretical quantiles) for each portfolio.
"""
# Generate samples
samples = dist.rvs(size=n_samples, random_state=random_state)
n_portfolios = weights.shape[0]
n_quantiles = len(quantiles)
empirical_quantiles = np.zeros((n_portfolios, n_quantiles))
theoretical_quantiles = np.zeros((n_portfolios, n_quantiles))
for i in range(n_portfolios):
w = weights[i]
test_proj = returns_test @ w
sample_proj = samples @ w
empirical_quantiles[i] = np.quantile(test_proj, quantiles)
theoretical_quantiles[i] = np.quantile(sample_proj, quantiles)
return empirical_quantiles, theoretical_quantiles, quantiles
[21]:
# Compute quantile comparisons for select distributions
quantile_results = {}
quantiles = np.linspace(0.01, 0.99, 99)
for name, dist in fitted_dists.items():
print(f"Computing quantiles for {name}...")
try:
emp_q, theo_q, q = compute_quantile_comparison(
dist, returns_test, random_weights,
quantiles=quantiles, n_samples=10000, random_state=42
)
quantile_results[name] = (emp_q, theo_q, q)
except Exception as e:
print(f" Error: {e}")
Computing quantiles for MVN...
Computing quantiles for VG...
Computing quantiles for NInvG...
Computing quantiles for NIG...
Computing quantiles for GH...
[22]:
# Create QQ plot comparing all distributions
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.flatten()
for idx, (name, (emp_q, theo_q, q)) in enumerate(quantile_results.items()):
if idx >= len(axes):
break
ax = axes[idx]
# Plot quantile range (5th-95th percentile across portfolios)
emp_median = np.median(emp_q, axis=0)
emp_lower = np.percentile(emp_q, 5, axis=0)
emp_upper = np.percentile(emp_q, 95, axis=0)
theo_median = np.median(theo_q, axis=0)
theo_lower = np.percentile(theo_q, 5, axis=0)
theo_upper = np.percentile(theo_q, 95, axis=0)
# Plot diagonal
min_val = min(emp_median.min(), theo_median.min())
max_val = max(emp_median.max(), theo_median.max())
ax.plot([min_val, max_val], [min_val, max_val], 'k--', alpha=0.5, label='Perfect fit')
# Plot median QQ line
ax.plot(theo_median, emp_median, 'b-', lw=2, label='Median')
# Plot confidence band
ax.fill_betweenx(emp_median, theo_lower, theo_upper, alpha=0.3,
label='5th-95th percentile range')
ax.set_xlabel('Theoretical Quantiles')
ax.set_ylabel('Empirical Quantiles')
ax.set_title(f'{name}')
ax.legend(loc='upper left', fontsize=8)
# Hide unused subplots
for idx in range(len(quantile_results), len(axes)):
axes[idx].set_visible(False)
plt.suptitle('QQ Plots: Theoretical vs Empirical Quantiles (Random Portfolio Projections)',
fontsize=14, y=1.02)
plt.tight_layout()
plt.savefig('qq_plots_comparison.png', dpi=150, bbox_inches='tight')
plt.show()
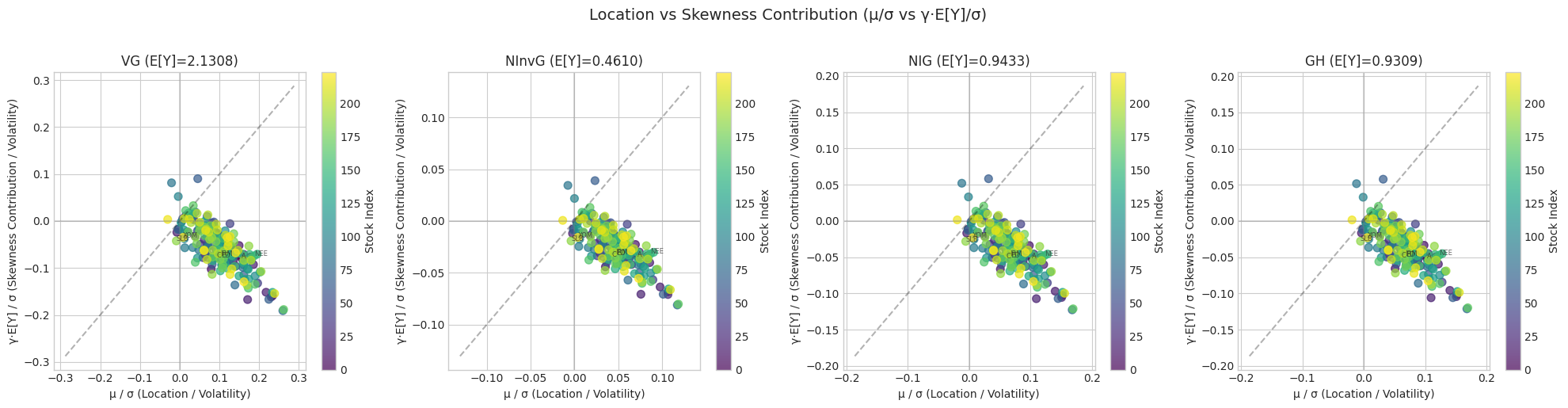
6. Parameter Analysis: Location (μ) vs Skewness (γ)
For normal mixture distributions, compare the location parameter μ and skewness parameter γ across stocks. We normalize by the volatility σ for comparison.
[27]:
# Extract parameters from fitted distributions
from normix.utils.bessel import log_kv
def compute_E_Y(name, params):
"""
Compute E[Y] for the mixing distribution of each normal mixture type.
- VG (Gamma): E[Y] = α / β (shape / rate)
- NInvG (InvGamma): E[Y] = β / (α - 1) for α > 1 (rate / (shape - 1))
- NIG (InvGaussian): E[Y] = δ (delta)
- GH (GIG): E[Y] = √(b/a) * K_{p+1}(√(ab)) / K_p(√(ab))
"""
if name == 'VG':
alpha = params['shape']
beta = params['rate']
return alpha / beta
elif name == 'NInvG':
alpha = params['shape']
beta = params['rate']
if alpha > 1:
return beta / (alpha - 1)
else:
return np.inf
elif name == 'NIG':
return params['delta']
elif name == 'GH':
p = params['p']
a = params['a']
b = params['b']
sqrt_ab = np.sqrt(a * b)
sqrt_b_over_a = np.sqrt(b / a) if a > 0 else np.inf
log_kv_p = log_kv(p, sqrt_ab)
log_kv_pp1 = log_kv(p + 1, sqrt_ab)
E_Y = sqrt_b_over_a * np.exp(log_kv_pp1 - log_kv_p)
return E_Y
else:
return 1.0 # Default for MVN or unknown
def extract_mixture_params(dist, name):
"""
Extract μ, γ, σ (diagonal of Σ), and E[Y] from normal mixture distributions.
Returns:
mu: Location parameter
gamma: Skewness parameter
sigma_diag: Diagonal of covariance (volatilities)
E_Y: Expected value of mixing variable
full_params: All classical parameters
mix_params: Mixing distribution parameters
"""
if name == 'MVN':
params = dist.classical_params
mu = params.mu
sigma_diag = np.sqrt(np.diag(params.sigma))
gamma = np.zeros_like(mu) # No skewness parameter for MVN
E_Y = 1.0 # MVN is not a mixture
return mu, gamma, sigma_diag, E_Y, None, None
else:
params = dist.classical_params
mu = params.mu
gamma = params.gamma
sigma_diag = np.sqrt(np.diag(params.sigma))
# Get mixing distribution parameters
if name == 'VG':
mix_params = {'shape': params.shape, 'rate': params.rate}
elif name == 'NInvG':
mix_params = {'shape': params.shape, 'rate': params.rate}
elif name == 'NIG':
mix_params = {'delta': params.delta, 'eta': params.eta}
elif name == 'GH':
mix_params = {'p': params.p, 'a': params.a, 'b': params.b}
else:
mix_params = None
# Compute E[Y]
E_Y = compute_E_Y(name, params)
return mu, gamma, sigma_diag, E_Y, params, mix_params
# Extract parameters for all mixture distributions
param_data = {}
for name, dist in fitted_dists.items():
try:
mu, gamma, sigma, E_Y, full_params, mix_params = extract_mixture_params(dist, name)
param_data[name] = {
'mu': mu,
'gamma': gamma,
'sigma': sigma,
'E_Y': E_Y,
'mu_over_sigma': mu / sigma,
'gamma_over_sigma': gamma / sigma,
'gamma_E_Y_over_sigma': gamma * E_Y / sigma, # The comparable quantity
'full_params': full_params,
'mix_params': mix_params
}
print(f"{name}: μ range [{mu.min():.6f}, {mu.max():.6f}], γ range [{gamma.min():.6f}, {gamma.max():.6f}], E[Y] = {E_Y:.6f}")
print(f" γ*E[Y] range [{(gamma*E_Y).min():.6f}, {(gamma*E_Y).max():.6f}]")
except Exception as e:
print(f"Error extracting params for {name}: {e}")
MVN: μ range [-0.000885, 0.002879], γ range [0.000000, 0.000000], E[Y] = 1.000000
γ*E[Y] range [0.000000, 0.000000]
VG: μ range [-0.000381, 0.004421], γ range [-0.000963, 0.000496], E[Y] = 2.130790
γ*E[Y] range [-0.002052, 0.001057]
NInvG: μ range [-0.000356, 0.004371], γ range [-0.004009, 0.002058], E[Y] = 0.460976
γ*E[Y] range [-0.001848, 0.000949]
NIG: μ range [-0.000369, 0.004393], γ range [-0.002111, 0.001086], E[Y] = 0.943274
γ*E[Y] range [-0.001992, 0.001025]
GH: μ range [-0.000369, 0.004396], γ range [-0.002117, 0.001089], E[Y] = 0.930902
γ*E[Y] range [-0.001971, 0.001014]
[28]:
# Create scatter plots comparing μ/σ vs γ*E[Y]/σ for each stock
# Note: For normal mixture X = μ + γY + √Y * Z, the contribution of γ to E[X] is γ*E[Y]
# So comparing μ/σ to γ*E[Y]/σ gives a better sense of relative contributions
mixture_dists = [n for n in ['VG', 'NInvG', 'NIG', 'GH'] if n in param_data]
if mixture_dists:
n_plots = len(mixture_dists)
fig, axes = plt.subplots(1, n_plots, figsize=(5*n_plots, 5))
if n_plots == 1:
axes = [axes]
for idx, name in enumerate(mixture_dists):
ax = axes[idx]
data = param_data[name]
mu_norm = data['mu_over_sigma']
gamma_E_Y_norm = data['gamma_E_Y_over_sigma'] # γ*E[Y]/σ instead of γ/σ
# Scatter plot
scatter = ax.scatter(mu_norm, gamma_E_Y_norm, c=range(len(mu_norm)),
cmap='viridis', s=50, alpha=0.7)
# Add diagonal line
lim = max(abs(mu_norm).max(), abs(gamma_E_Y_norm).max()) * 1.1
if np.isfinite(lim) and lim > 0:
ax.plot([-lim, lim], [-lim, lim], 'k--', alpha=0.3, label='μ = γE[Y]')
ax.axhline(0, color='gray', linestyle='-', alpha=0.3)
ax.axvline(0, color='gray', linestyle='-', alpha=0.3)
# Labels
ax.set_xlabel('μ / σ (Location / Volatility)')
ax.set_ylabel('γ·E[Y] / σ (Skewness Contribution / Volatility)')
ax.set_title(f'{name} (E[Y]={data["E_Y"]:.4f})')
# Add colorbar to show stock index
plt.colorbar(scatter, ax=ax, label='Stock Index')
# Add labels for a few interesting points
n_labels = min(len(selected_tickers), 6) # Label up to 6 stocks
step = max(1, len(selected_tickers) // n_labels)
for i, ticker in enumerate(selected_tickers):
if i % step == 0:
ax.annotate(ticker, (mu_norm[i], gamma_E_Y_norm[i]), fontsize=6, alpha=0.7)
plt.suptitle('Location vs Skewness Contribution (μ/σ vs γ·E[Y]/σ)', fontsize=14, y=1.02)
plt.tight_layout()
plt.savefig('mu_vs_gamma_E_Y_scatter.png', dpi=150, bbox_inches='tight')
plt.show()
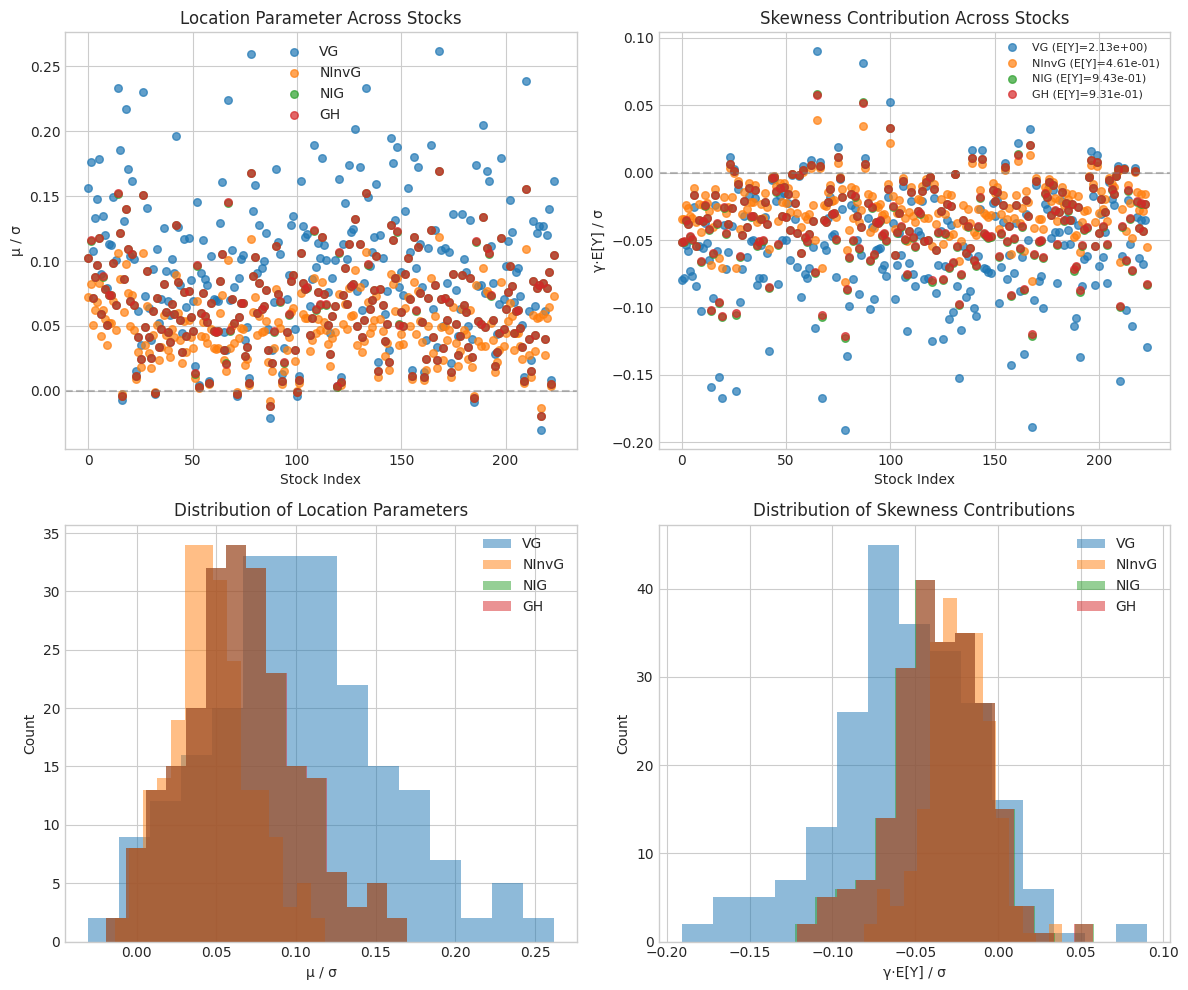
[29]:
# Create combined comparison plot using γ*E[Y]/σ for fair comparison
if len(mixture_dists) >= 2:
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
# Plot 1: μ/σ comparison across distributions
ax1 = axes[0, 0]
for name in mixture_dists:
data = param_data[name]
ax1.scatter(range(len(data['mu_over_sigma'])), data['mu_over_sigma'],
label=name, alpha=0.7, s=30)
ax1.set_xlabel('Stock Index')
ax1.set_ylabel('μ / σ')
ax1.set_title('Location Parameter Across Stocks')
ax1.legend()
ax1.axhline(0, color='gray', linestyle='--', alpha=0.5)
# Plot 2: γ*E[Y]/σ comparison across distributions (scaled skewness contribution)
ax2 = axes[0, 1]
for name in mixture_dists:
data = param_data[name]
ax2.scatter(range(len(data['gamma_E_Y_over_sigma'])), data['gamma_E_Y_over_sigma'],
label=f"{name} (E[Y]={data['E_Y']:.2e})", alpha=0.7, s=30)
ax2.set_xlabel('Stock Index')
ax2.set_ylabel('γ·E[Y] / σ')
ax2.set_title('Skewness Contribution Across Stocks')
ax2.legend(fontsize=8)
ax2.axhline(0, color='gray', linestyle='--', alpha=0.5)
# Plot 3: μ/σ histograms
ax3 = axes[1, 0]
for name in mixture_dists:
data = param_data[name]
ax3.hist(data['mu_over_sigma'], bins=15, alpha=0.5, label=name)
ax3.set_xlabel('μ / σ')
ax3.set_ylabel('Count')
ax3.set_title('Distribution of Location Parameters')
ax3.legend()
# Plot 4: γ*E[Y]/σ histograms (scaled skewness contribution)
ax4 = axes[1, 1]
for name in mixture_dists:
data = param_data[name]
ax4.hist(data['gamma_E_Y_over_sigma'], bins=15, alpha=0.5, label=name)
ax4.set_xlabel('γ·E[Y] / σ')
ax4.set_ylabel('Count')
ax4.set_title('Distribution of Skewness Contributions')
ax4.legend()
plt.tight_layout()
plt.savefig('parameter_comparison.png', dpi=150, bbox_inches='tight')
plt.show()
[30]:
# Compare Mean, Variance, and Skewness from Estimated Distributions
# For normal variance-mean mixture X = μ + γY + √Y·ε where ε ~ N(0, Σ):
# - E[X] = μ + γE[Y]
# - Var[X]_i = E[Y]·Σ_ii + Var[Y]·γ_i²
def compute_Var_Y(name, params):
"""
Compute Var[Y] for the mixing distribution.
- VG (Gamma): Var[Y] = α / β² (shape / rate²)
- NInvG (InvGamma): Var[Y] = β² / ((α-1)²(α-2)) for α > 2
- NIG (InvGaussian): Var[Y] = δ³ / η (delta³ / eta)
- GH (GIG): Var[Y] = E[Y²] - E[Y]² computed via Bessel ratios
"""
if name == 'VG':
alpha = params['shape']
beta = params['rate']
return alpha / (beta ** 2)
elif name == 'NInvG':
alpha = params['shape']
beta = params['rate']
if alpha > 2:
return (beta ** 2) / ((alpha - 1) ** 2 * (alpha - 2))
else:
return np.inf
elif name == 'NIG':
delta = params['delta']
eta = params['eta']
return (delta ** 3) / eta
elif name == 'GH':
p = params['p']
a = params['a']
b = params['b']
sqrt_ab = np.sqrt(a * b)
sqrt_b_over_a = np.sqrt(b / a) if a > 0 else np.inf
log_kv_p = log_kv(p, sqrt_ab)
log_kv_pp1 = log_kv(p + 1, sqrt_ab)
log_kv_pp2 = log_kv(p + 2, sqrt_ab)
E_Y = sqrt_b_over_a * np.exp(log_kv_pp1 - log_kv_p)
E_Y2 = (b / a) * np.exp(log_kv_pp2 - log_kv_p)
return E_Y2 - E_Y ** 2
else:
return 0.0
print("="*80)
print("MOMENT COMPARISON FROM ESTIMATED DISTRIBUTIONS")
print("="*80)
# Compare empirical moments with distribution moments
empirical_mean = returns_train.mean(axis=0)
empirical_var = returns_train.var(axis=0)
empirical_skew = stats.skew(returns_train, axis=0)
moment_comparison = {}
for name in mixture_dists:
data = param_data[name]
mu = data['mu']
gamma = data['gamma']
sigma_diag_sq = data['sigma'] ** 2 # Variance (diagonal of Σ)
E_Y = data['E_Y']
Var_Y = compute_Var_Y(name, data['full_params'])
# Compute distribution mean: E[X] = μ + γE[Y]
dist_mean = mu + gamma * E_Y
# Compute distribution variance: Var[X]_i = E[Y]·Σ_ii + Var[Y]·γ_i²
dist_var = E_Y * sigma_diag_sq + Var_Y * (gamma ** 2)
moment_comparison[name] = {
'E_Y': E_Y,
'Var_Y': Var_Y,
'dist_mean': dist_mean,
'dist_var': dist_var,
'dist_std': np.sqrt(dist_var),
'mean_error': np.mean(np.abs(dist_mean - empirical_mean)),
'var_error': np.mean(np.abs(dist_var - empirical_var))
}
print(f"\n{name}:")
print(f" E[Y] = {E_Y:.6e}, Var[Y] = {Var_Y:.6e}")
print(f" Mean: Dist avg = {dist_mean.mean():.6e}, Empirical avg = {empirical_mean.mean():.6e}")
print(f" MAE = {moment_comparison[name]['mean_error']:.6e}")
print(f" Var: Dist avg = {dist_var.mean():.6e}, Empirical avg = {empirical_var.mean():.6e}")
print(f" MAE = {moment_comparison[name]['var_error']:.6e}")
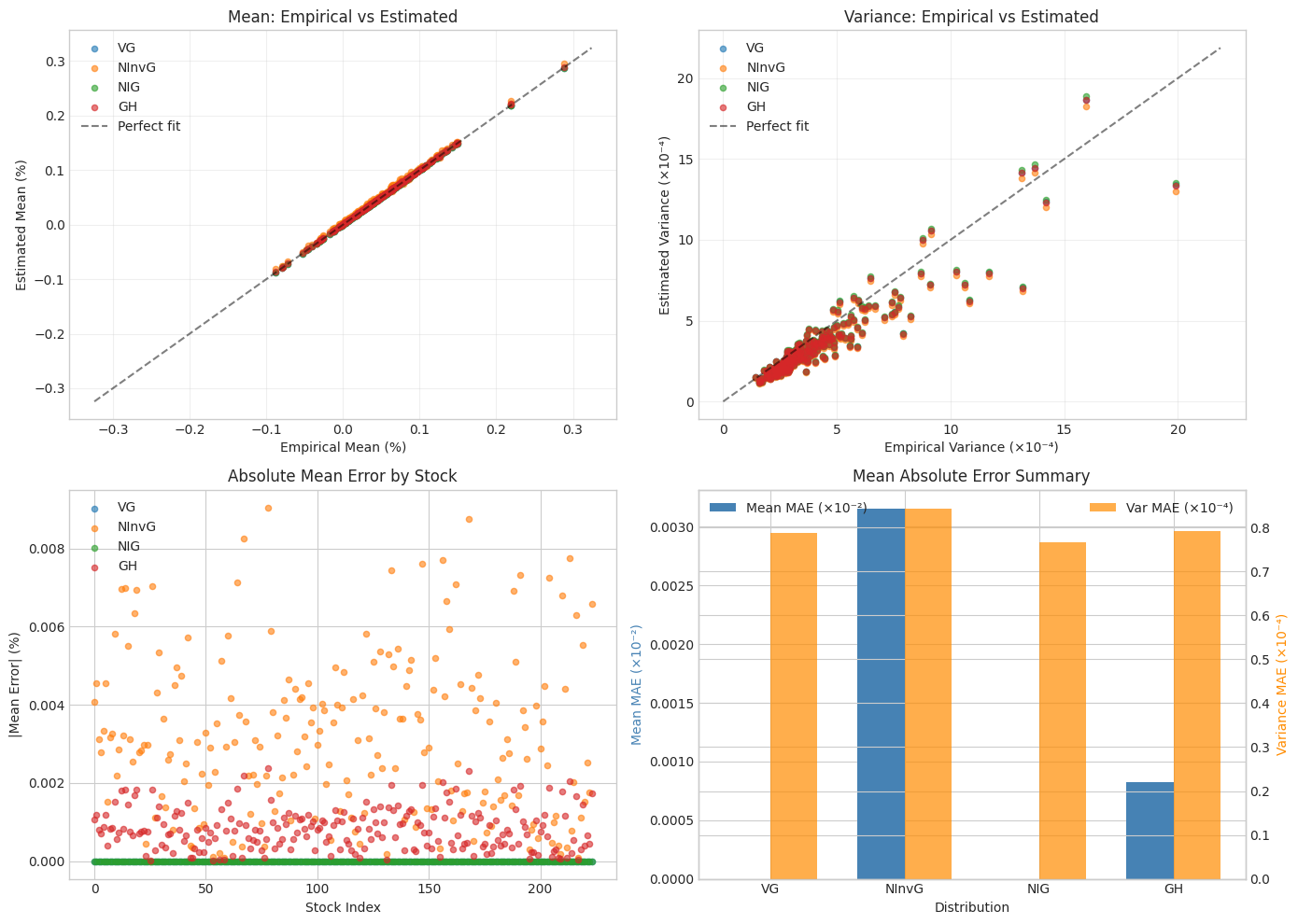
# Create comparison visualization
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# Plot 1: Mean comparison (scatter: empirical vs estimated)
ax1 = axes[0, 0]
for name in mixture_dists:
mc = moment_comparison[name]
ax1.scatter(empirical_mean * 100, mc['dist_mean'] * 100, label=name, alpha=0.6, s=20)
# Add diagonal line
lim = max(abs(empirical_mean).max(), max(abs(mc['dist_mean']).max() for mc in moment_comparison.values())) * 100 * 1.1
ax1.plot([-lim, lim], [-lim, lim], 'k--', alpha=0.5, label='Perfect fit')
ax1.set_xlabel('Empirical Mean (%)')
ax1.set_ylabel('Estimated Mean (%)')
ax1.set_title('Mean: Empirical vs Estimated')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Plot 2: Variance comparison (scatter: empirical vs estimated)
ax2 = axes[0, 1]
for name in mixture_dists:
mc = moment_comparison[name]
ax2.scatter(empirical_var * 10000, mc['dist_var'] * 10000, label=name, alpha=0.6, s=20)
lim = max(empirical_var.max(), max(mc['dist_var'].max() for mc in moment_comparison.values() if np.isfinite(mc['dist_var']).all())) * 10000 * 1.1
ax2.plot([0, lim], [0, lim], 'k--', alpha=0.5, label='Perfect fit')
ax2.set_xlabel('Empirical Variance (×10⁻⁴)')
ax2.set_ylabel('Estimated Variance (×10⁻⁴)')
ax2.set_title('Variance: Empirical vs Estimated')
ax2.legend()
ax2.grid(True, alpha=0.3)
# Plot 3: Mean error by stock
ax3 = axes[1, 0]
for name in mixture_dists:
mc = moment_comparison[name]
mean_errors = np.abs(mc['dist_mean'] - empirical_mean) * 100
ax3.scatter(range(len(mean_errors)), mean_errors, label=name, alpha=0.6, s=20)
ax3.set_xlabel('Stock Index')
ax3.set_ylabel('|Mean Error| (%)')
ax3.set_title('Absolute Mean Error by Stock')
ax3.legend()
# Plot 4: Summary statistics
ax4 = axes[1, 1]
names = list(moment_comparison.keys())
mean_maes = [moment_comparison[n]['mean_error'] * 100 for n in names]
var_maes = [moment_comparison[n]['var_error'] * 10000 for n in names]
x = np.arange(len(names))
width = 0.35
bars1 = ax4.bar(x - width/2, mean_maes, width, label='Mean MAE (×10⁻²)', color='steelblue')
ax4_twin = ax4.twinx()
bars2 = ax4_twin.bar(x + width/2, var_maes, width, label='Var MAE (×10⁻⁴)', color='darkorange', alpha=0.7)
ax4.set_xlabel('Distribution')
ax4.set_ylabel('Mean MAE (×10⁻²)', color='steelblue')
ax4_twin.set_ylabel('Variance MAE (×10⁻⁴)', color='darkorange')
ax4.set_xticks(x)
ax4.set_xticklabels(names)
ax4.set_title('Mean Absolute Error Summary')
ax4.legend(loc='upper left')
ax4_twin.legend(loc='upper right')
plt.tight_layout()
plt.savefig('moment_comparison.png', dpi=150, bbox_inches='tight')
plt.show()
# Print summary table
print("\n" + "="*80)
print("SUMMARY TABLE: Distribution Moment Comparison")
print("="*80)
summary_df = pd.DataFrame({
'Distribution': names,
'E[Y]': [moment_comparison[n]['E_Y'] for n in names],
'Var[Y]': [moment_comparison[n]['Var_Y'] for n in names],
'Mean MAE': [moment_comparison[n]['mean_error'] for n in names],
'Var MAE': [moment_comparison[n]['var_error'] for n in names]
})
print(summary_df.to_string(index=False))
================================================================================
MOMENT COMPARISON FROM ESTIMATED DISTRIBUTIONS
================================================================================
VG:
E[Y] = 2.130790e+00, Var[Y] = 2.229780e+00
Mean: Dist avg = 5.226405e-04, Empirical avg = 5.226405e-04
MAE = 2.464937e-17
Var: Dist avg = 3.526543e-04, Empirical avg = 4.178537e-04
MAE = 7.873155e-05
NInvG:
E[Y] = 4.609764e-01, Var[Y] = 2.382077e-01
Mean: Dist avg = 5.522672e-04, Empirical avg = 5.226405e-04
MAE = 3.157227e-05
Var: Dist avg = 3.439041e-04, Empirical avg = 4.178537e-04
MAE = 8.438055e-05
NIG:
E[Y] = 9.432736e-01, Var[Y] = 5.249672e-01
Mean: Dist avg = 5.226405e-04, Empirical avg = 5.226405e-04
MAE = 1.786790e-17
Var: Dist avg = 3.567892e-04, Empirical avg = 4.178537e-04
MAE = 7.660339e-05
GH:
E[Y] = 9.309021e-01, Var[Y] = 4.867629e-01
Mean: Dist avg = 5.303291e-04, Empirical avg = 5.226405e-04
MAE = 8.222104e-06
Var: Dist avg = 3.521624e-04, Empirical avg = 4.178537e-04
MAE = 7.925527e-05
================================================================================
SUMMARY TABLE: Distribution Moment Comparison
================================================================================
Distribution E[Y] Var[Y] Mean MAE Var MAE
VG 2.130790 2.229780 2.464937e-17 0.000079
NInvG 0.460976 0.238208 3.157227e-05 0.000084
NIG 0.943274 0.524967 1.786790e-17 0.000077
GH 0.930902 0.486763 8.222104e-06 0.000079
[31]:
# Create a detailed parameter table for one distribution (e.g., GH)
best_dist = 'GH' if 'GH' in param_data else list(param_data.keys())[-1]
if best_dist in param_data:
data = param_data[best_dist]
param_table = pd.DataFrame({
'Ticker': selected_tickers,
'μ': data['mu'],
'γ': data['gamma'],
'γ·E[Y]': data['gamma'] * data['E_Y'], # Skewness contribution
'σ': data['sigma'],
'μ/σ': data['mu_over_sigma'],
'γ/σ': data['gamma_over_sigma'],
'γ·E[Y]/σ': data['gamma_E_Y_over_sigma'] # Comparable skewness measure
})
# Sort by γ*E[Y]/σ to see which stocks have most skewness contribution
param_table_sorted = param_table.sort_values('γ·E[Y]/σ')
print(f"\n{best_dist} Parameters by Stock (sorted by skewness contribution γ·E[Y]/σ):")
print(f"Note: E[Y] = {data['E_Y']:.6e}")
print("="*100)
print(param_table_sorted.to_string(index=False))
print("="*100)
# Print mixing distribution parameters
if data['mix_params']:
print(f"\n{best_dist} Mixing Distribution Parameters:")
for k, v in data['mix_params'].items():
if isinstance(v, float):
print(f" {k}: {v:.6e}")
else:
print(f" {k}: {v}")
GH Parameters by Stock (sorted by skewness contribution γ·E[Y]/σ):
Note: E[Y] = 9.309021e-01
====================================================================================================
Ticker μ γ γ·E[Y] σ μ/σ γ/σ γ·E[Y]/σ
EQIX 0.002732 -0.002117 -0.001971 0.016250 0.168124 -0.130298 -0.121294
PLD 0.002697 -0.002047 -0.001905 0.015900 0.169643 -0.128726 -0.119831
AVB 0.001572 -0.001632 -0.001519 0.014332 0.109678 -0.113883 -0.106014
DLR 0.002471 -0.001936 -0.001802 0.017023 0.145175 -0.113722 -0.105864
BAX 0.002180 -0.001620 -0.001508 0.014438 0.150969 -0.112205 -0.104452
AMT 0.002267 -0.001627 -0.001515 0.014909 0.152069 -0.109153 -0.101611
V 0.002322 -0.001581 -0.001472 0.014910 0.155760 -0.106027 -0.098701
MCO 0.002518 -0.001727 -0.001608 0.016513 0.152459 -0.104580 -0.097354
ARE 0.002036 -0.001493 -0.001389 0.014504 0.140361 -0.102904 -0.095794
O 0.001797 -0.001570 -0.001461 0.016166 0.111162 -0.097088 -0.090379
STZ 0.001997 -0.001702 -0.001585 0.018145 0.110075 -0.093823 -0.087340
PEP 0.001399 -0.001050 -0.000978 0.011309 0.123745 -0.092881 -0.086463
EQR 0.001334 -0.001387 -0.001292 0.015030 0.088731 -0.092311 -0.085933
CCI 0.001874 -0.001332 -0.001240 0.014684 0.127649 -0.090706 -0.084438
ZBH 0.001811 -0.001532 -0.001426 0.017278 0.104799 -0.088642 -0.082517
KO 0.001222 -0.000984 -0.000916 0.011452 0.106712 -0.085904 -0.079968
LMT 0.001580 -0.001186 -0.001104 0.013962 0.113161 -0.084938 -0.079069
MDLZ 0.001393 -0.001155 -0.001075 0.014290 0.097484 -0.080795 -0.075212
ICE 0.001774 -0.001155 -0.001075 0.014357 0.123588 -0.080427 -0.074869
DHI 0.002192 -0.001652 -0.001538 0.020822 0.105276 -0.079321 -0.073840
WELL 0.001554 -0.001477 -0.001375 0.018990 0.081835 -0.077775 -0.072401
SPG 0.001088 -0.001631 -0.001518 0.021141 0.051467 -0.077130 -0.071801
MA 0.002202 -0.001246 -0.001160 0.016652 0.132255 -0.074842 -0.069671
SPGI 0.002147 -0.001185 -0.001103 0.016006 0.134159 -0.074051 -0.068934
MO 0.001023 -0.001128 -0.001050 0.015396 0.066440 -0.073286 -0.068222
MCD 0.001392 -0.000879 -0.000818 0.012290 0.113236 -0.071493 -0.066553
AIG 0.000979 -0.001355 -0.001261 0.019193 0.051021 -0.070595 -0.065717
FIS 0.001635 -0.001023 -0.000952 0.014644 0.111645 -0.069834 -0.065009
MMM 0.001162 -0.001032 -0.000960 0.014796 0.078518 -0.069717 -0.064899
VRTX 0.002219 -0.001820 -0.001694 0.026254 0.084504 -0.069306 -0.064518
ES 0.001361 -0.000889 -0.000828 0.013156 0.103473 -0.067569 -0.062900
PSA 0.001003 -0.000989 -0.000920 0.014670 0.068347 -0.067403 -0.062746
NOC 0.001381 -0.001019 -0.000949 0.015285 0.090336 -0.066674 -0.062067
BDX 0.001380 -0.000995 -0.000926 0.014946 0.092338 -0.066557 -0.061958
HD 0.001503 -0.000921 -0.000858 0.014127 0.106411 -0.065214 -0.060708
PM 0.001116 -0.001026 -0.000955 0.015773 0.070738 -0.065070 -0.060574
GD 0.001016 -0.000955 -0.000889 0.014742 0.068937 -0.064767 -0.060291
AMZN 0.002434 -0.001279 -0.001191 0.020011 0.121648 -0.063916 -0.059500
CVS 0.000986 -0.001187 -0.001105 0.018650 0.052868 -0.063645 -0.059247
MET 0.001381 -0.001259 -0.001172 0.019795 0.069788 -0.063618 -0.059223
LEN 0.001626 -0.001352 -0.001259 0.022065 0.073712 -0.061272 -0.057038
OXY 0.000671 -0.001652 -0.001538 0.027419 0.024487 -0.060244 -0.056081
EXR 0.001270 -0.000981 -0.000913 0.016287 0.078008 -0.060225 -0.056063
MKC 0.001488 -0.000857 -0.000797 0.014335 0.103816 -0.059761 -0.055632
MCK 0.001131 -0.001218 -0.001134 0.020780 0.054418 -0.058632 -0.054580
ISRG 0.002259 -0.001114 -0.001037 0.019096 0.118292 -0.058347 -0.054315
AEP 0.001120 -0.000738 -0.000687 0.012701 0.088154 -0.058070 -0.054058
TMO 0.001859 -0.000914 -0.000851 0.015750 0.118044 -0.058033 -0.054023
SYK 0.001642 -0.000897 -0.000835 0.015508 0.105871 -0.057843 -0.053846
BSX 0.001485 -0.001038 -0.000966 0.018023 0.082368 -0.057570 -0.053592
UAL 0.001311 -0.001666 -0.001551 0.029172 0.044947 -0.057100 -0.053154
CL 0.000951 -0.000709 -0.000660 0.012438 0.076432 -0.056963 -0.053027
RTX 0.001089 -0.000934 -0.000870 0.016431 0.066274 -0.056848 -0.052920
A 0.001762 -0.000945 -0.000879 0.017206 0.102394 -0.054908 -0.051114
PPG 0.001177 -0.000904 -0.000842 0.016506 0.071295 -0.054778 -0.050993
AAPL 0.002220 -0.001045 -0.000973 0.019162 0.115872 -0.054547 -0.050778
NVDA 0.003874 -0.001784 -0.001661 0.032714 0.118435 -0.054539 -0.050771
C 0.001262 -0.001137 -0.001058 0.020852 0.060513 -0.054521 -0.050754
DAL 0.001126 -0.001320 -0.001228 0.024302 0.046323 -0.054302 -0.050550
KHC 0.000507 -0.000966 -0.000899 0.017869 0.028381 -0.054043 -0.050309
GOOGL 0.001484 -0.000895 -0.000834 0.016625 0.089292 -0.053864 -0.050142
ETR 0.001158 -0.000753 -0.000701 0.013986 0.082796 -0.053838 -0.050118
PRU 0.001114 -0.001091 -0.001015 0.020330 0.054810 -0.053656 -0.049949
CAH 0.000774 -0.001100 -0.001024 0.020535 0.037678 -0.053557 -0.049856
KMB 0.000888 -0.000726 -0.000675 0.013581 0.065409 -0.053424 -0.049733
ADBE 0.002312 -0.001047 -0.000975 0.019677 0.117509 -0.053227 -0.049549
IBM 0.000867 -0.000820 -0.000763 0.015441 0.056130 -0.053089 -0.049421
ED 0.000877 -0.000685 -0.000637 0.012897 0.067963 -0.053080 -0.049412
OKE 0.001942 -0.001348 -0.001255 0.025807 0.075261 -0.052251 -0.048640
MU 0.002923 -0.001735 -0.001615 0.033660 0.086840 -0.051535 -0.047974
IRM 0.001178 -0.000911 -0.000848 0.017674 0.066628 -0.051521 -0.047961
D 0.000894 -0.000681 -0.000634 0.013227 0.067620 -0.051495 -0.047936
NEE 0.001577 -0.000651 -0.000606 0.012842 0.122822 -0.050710 -0.047206
ACN 0.001475 -0.000768 -0.000715 0.015193 0.097062 -0.050540 -0.047048
MSFT 0.001930 -0.000826 -0.000769 0.016629 0.116051 -0.049702 -0.046268
GM 0.001240 -0.001045 -0.000973 0.021068 0.058872 -0.049621 -0.046192
BIIB 0.001039 -0.001234 -0.001149 0.025054 0.041455 -0.049258 -0.045855
DD 0.000901 -0.000962 -0.000896 0.019746 0.045623 -0.048719 -0.045352
MSCI 0.002315 -0.000876 -0.000816 0.018103 0.127866 -0.048406 -0.045061
AWK 0.001448 -0.000664 -0.000619 0.013753 0.105292 -0.048313 -0.044975
NOW 0.002555 -0.001204 -0.001121 0.024948 0.102428 -0.048274 -0.044938
GOOG 0.001409 -0.000803 -0.000747 0.016646 0.084667 -0.048223 -0.044891
LOW 0.001496 -0.000891 -0.000829 0.018486 0.080918 -0.048176 -0.044847
CSCO 0.001296 -0.000821 -0.000764 0.017133 0.075643 -0.047904 -0.044594
TRV 0.000881 -0.000670 -0.000623 0.013997 0.062944 -0.047843 -0.044537
HLT 0.001555 -0.000888 -0.000826 0.018648 0.083406 -0.047596 -0.044307
LIN 0.001460 -0.000725 -0.000675 0.015371 0.094953 -0.047196 -0.043935
XEL 0.001166 -0.000589 -0.000548 0.012729 0.091638 -0.046238 -0.043043
INTC 0.001254 -0.000923 -0.000859 0.019972 0.062772 -0.046204 -0.043012
COST 0.001391 -0.000656 -0.000611 0.014393 0.096610 -0.045602 -0.042451
SYY 0.001284 -0.000786 -0.000731 0.017464 0.073502 -0.044992 -0.041884
AMGN 0.001091 -0.000740 -0.000689 0.016495 0.066125 -0.044881 -0.041780
WMB 0.001168 -0.001282 -0.001194 0.029333 0.039835 -0.043714 -0.040694
T 0.000755 -0.000598 -0.000557 0.013768 0.054870 -0.043463 -0.040460
BKNG 0.001199 -0.000845 -0.000787 0.019573 0.061271 -0.043192 -0.040208
F 0.000618 -0.000836 -0.000778 0.019486 0.031705 -0.042891 -0.039927
TTWO 0.002347 -0.001046 -0.000974 0.024457 0.095949 -0.042768 -0.039813
MPC 0.001074 -0.001189 -0.001107 0.027802 0.038617 -0.042755 -0.039800
META 0.001533 -0.000841 -0.000783 0.019729 0.077708 -0.042632 -0.039686
VLO 0.000958 -0.001024 -0.000953 0.024033 0.039858 -0.042595 -0.039652
HSY 0.001065 -0.000569 -0.000530 0.013364 0.079708 -0.042580 -0.039638
PEG 0.000987 -0.000586 -0.000545 0.013757 0.071755 -0.042562 -0.039621
NXPI 0.001440 -0.000978 -0.000910 0.023230 0.061997 -0.042098 -0.039189
CB 0.000846 -0.000582 -0.000542 0.014301 0.059168 -0.040698 -0.037886
AXP 0.001123 -0.000687 -0.000640 0.016892 0.066495 -0.040689 -0.037878
ABT 0.001372 -0.000636 -0.000592 0.015634 0.087727 -0.040683 -0.037872
APD 0.001260 -0.000588 -0.000548 0.014666 0.085902 -0.040106 -0.037334
GILD 0.000398 -0.000725 -0.000675 0.018148 0.021909 -0.039933 -0.037174
GE 0.000195 -0.000973 -0.000906 0.024830 0.007842 -0.039187 -0.036479
DTE 0.000932 -0.000512 -0.000476 0.013091 0.071166 -0.039100 -0.036398
ALL 0.000980 -0.000509 -0.000474 0.013247 0.073999 -0.038417 -0.035763
DG 0.001553 -0.000700 -0.000651 0.018308 0.084844 -0.038219 -0.035578
GIS 0.000686 -0.000573 -0.000533 0.015073 0.045492 -0.037992 -0.035367
SHW 0.001385 -0.000602 -0.000560 0.015891 0.087141 -0.037857 -0.035241
ABBV 0.001338 -0.000710 -0.000661 0.018755 0.071316 -0.037839 -0.035224
MDT 0.000914 -0.000543 -0.000506 0.014441 0.063265 -0.037628 -0.035028
AES 0.001586 -0.000759 -0.000706 0.020194 0.078516 -0.037579 -0.034982
DLTR 0.001010 -0.000815 -0.000758 0.021700 0.046566 -0.037540 -0.034946
SNPS 0.001948 -0.000631 -0.000588 0.016921 0.115115 -0.037317 -0.034738
CAG 0.000884 -0.000721 -0.000671 0.019531 0.045272 -0.036902 -0.034352
WEC 0.001031 -0.000471 -0.000438 0.012958 0.079573 -0.036310 -0.033801
AMD 0.004396 -0.001610 -0.001499 0.044745 0.098241 -0.035980 -0.033494
COF 0.000979 -0.000747 -0.000695 0.021300 0.045962 -0.035053 -0.032631
BLK 0.001234 -0.000599 -0.000558 0.017174 0.071823 -0.034874 -0.032464
PG 0.000942 -0.000398 -0.000371 0.011539 0.081673 -0.034528 -0.032142
CME 0.001161 -0.000519 -0.000483 0.015035 0.077201 -0.034524 -0.032138
BMY 0.000624 -0.000631 -0.000587 0.018327 0.034066 -0.034411 -0.032033
EXC 0.000954 -0.000502 -0.000468 0.014647 0.065155 -0.034298 -0.031928
REGN 0.000681 -0.000827 -0.000770 0.024656 0.027616 -0.033546 -0.031228
EA 0.001245 -0.000711 -0.000662 0.021763 0.057206 -0.032662 -0.030406
JNJ 0.000809 -0.000391 -0.000364 0.012143 0.066608 -0.032202 -0.029977
ECL 0.000942 -0.000447 -0.000416 0.013949 0.067501 -0.032068 -0.029853
HON 0.001099 -0.000445 -0.000414 0.013966 0.078709 -0.031865 -0.029663
TXN 0.001454 -0.000558 -0.000519 0.018001 0.080791 -0.031000 -0.028858
SBUX 0.000931 -0.000475 -0.000442 0.015324 0.060786 -0.030995 -0.028853
LLY 0.001100 -0.000502 -0.000467 0.016426 0.066949 -0.030560 -0.028448
ITW 0.001159 -0.000471 -0.000438 0.015581 0.074415 -0.030232 -0.028143
SLB -0.000129 -0.000705 -0.000657 0.023589 -0.005484 -0.029906 -0.027840
RSG 0.000989 -0.000330 -0.000308 0.011088 0.089237 -0.029800 -0.027741
BA 0.000981 -0.000667 -0.000621 0.023712 0.041379 -0.028147 -0.026202
AVGO 0.001555 -0.000621 -0.000578 0.022465 0.069237 -0.027639 -0.025729
FTNT 0.001788 -0.000654 -0.000609 0.023825 0.075025 -0.027468 -0.025570
SRE 0.000713 -0.000390 -0.000363 0.014448 0.049322 -0.026992 -0.025127
HAL 0.000227 -0.000746 -0.000695 0.027851 0.008163 -0.026793 -0.024941
MAR 0.001041 -0.000550 -0.000512 0.020690 0.050294 -0.026588 -0.024750
AMAT 0.001864 -0.000654 -0.000609 0.025178 0.074037 -0.025964 -0.024170
ORCL 0.000848 -0.000414 -0.000385 0.016009 0.052964 -0.025857 -0.024070
NSC 0.001295 -0.000469 -0.000436 0.018322 0.070670 -0.025574 -0.023807
SO 0.000697 -0.000320 -0.000298 0.013029 0.053529 -0.024579 -0.022881
XOM 0.000091 -0.000400 -0.000372 0.016267 0.005606 -0.024571 -0.022873
LRCX 0.002068 -0.000617 -0.000575 0.025148 0.082245 -0.024550 -0.022854
WMT 0.001132 -0.000351 -0.000327 0.014340 0.078938 -0.024474 -0.022783
CRM 0.001288 -0.000520 -0.000484 0.021490 0.059921 -0.024218 -0.022544
FDX 0.000941 -0.000496 -0.000461 0.020536 0.045798 -0.024134 -0.022466
SJM 0.000427 -0.000387 -0.000361 0.016271 0.026216 -0.023814 -0.022168
DUK 0.000647 -0.000284 -0.000265 0.012360 0.052350 -0.023013 -0.021423
CAT 0.001350 -0.000462 -0.000430 0.020097 0.067196 -0.023003 -0.021413
WM 0.000952 -0.000260 -0.000242 0.011398 0.083487 -0.022770 -0.021196
NFLX 0.001739 -0.000649 -0.000605 0.028627 0.060758 -0.022687 -0.021120
BK 0.000437 -0.000384 -0.000358 0.017224 0.025351 -0.022303 -0.020762
PFE 0.000569 -0.000295 -0.000275 0.013732 0.041426 -0.021483 -0.019998
TSLA 0.002960 -0.000820 -0.000764 0.038982 0.075926 -0.021044 -0.019590
MRK 0.000719 -0.000275 -0.000256 0.013957 0.051520 -0.019732 -0.018368
PYPL 0.001858 -0.000400 -0.000372 0.020574 0.090323 -0.019432 -0.018089
EOG 0.000167 -0.000501 -0.000466 0.026227 0.006372 -0.019096 -0.017776
EW 0.001302 -0.000390 -0.000363 0.020673 0.062975 -0.018848 -0.017545
ADI 0.001158 -0.000349 -0.000325 0.019525 0.059312 -0.017877 -0.016642
APA -0.000147 -0.000675 -0.000629 0.037888 -0.003867 -0.017821 -0.016590
ETN 0.001021 -0.000287 -0.000267 0.016973 0.060156 -0.016910 -0.015741
UPS 0.000753 -0.000260 -0.000242 0.015462 0.048723 -0.016814 -0.015652
COP 0.000344 -0.000429 -0.000399 0.025642 0.013428 -0.016722 -0.015566
PSX 0.000297 -0.000339 -0.000315 0.020497 0.014510 -0.016523 -0.015382
INTU 0.001344 -0.000275 -0.000256 0.017556 0.076529 -0.015646 -0.014565
SCHW 0.000741 -0.000345 -0.000321 0.022094 0.033535 -0.015603 -0.014525
NKE 0.000917 -0.000279 -0.000260 0.018363 0.049930 -0.015218 -0.014166
CI 0.000601 -0.000299 -0.000279 0.020070 0.029954 -0.014915 -0.013885
JPM 0.000859 -0.000250 -0.000233 0.016927 0.050736 -0.014777 -0.013756
VZ 0.000547 -0.000179 -0.000167 0.012658 0.043252 -0.014172 -0.013192
BRK-B 0.000597 -0.000175 -0.000163 0.012566 0.047487 -0.013918 -0.012956
NEM 0.001315 -0.000352 -0.000327 0.025713 0.051150 -0.013674 -0.012729
UNP 0.001055 -0.000226 -0.000210 0.016905 0.062432 -0.013351 -0.012428
DVN -0.000074 -0.000481 -0.000448 0.036368 -0.002047 -0.013223 -0.012309
GS 0.000600 -0.000247 -0.000230 0.018864 0.031815 -0.013085 -0.012181
KR 0.000147 -0.000285 -0.000265 0.021919 0.006698 -0.012992 -0.012094
TJX 0.000747 -0.000209 -0.000194 0.016821 0.044394 -0.012420 -0.011562
CMCSA 0.000689 -0.000197 -0.000183 0.016250 0.042376 -0.012102 -0.011266
BKR -0.000042 -0.000319 -0.000297 0.026913 -0.001551 -0.011844 -0.011026
CMI 0.001012 -0.000201 -0.000187 0.017724 0.057116 -0.011321 -0.010539
ROST 0.000820 -0.000191 -0.000178 0.019362 0.042330 -0.009864 -0.009182
BBY 0.001275 -0.000236 -0.000220 0.025880 0.049268 -0.009138 -0.008506
KLAC 0.001312 -0.000167 -0.000155 0.022834 0.057455 -0.007302 -0.006798
QCOM 0.001165 -0.000162 -0.000151 0.022647 0.051456 -0.007152 -0.006658
PNC 0.000588 -0.000118 -0.000110 0.017839 0.032976 -0.006599 -0.006143
HUM 0.000840 -0.000127 -0.000118 0.019460 0.043145 -0.006538 -0.006087
UNH 0.001020 -0.000092 -0.000085 0.016564 0.061564 -0.005543 -0.005160
CDNS 0.001537 -0.000082 -0.000076 0.018270 0.084126 -0.004489 -0.004178
EMR 0.000586 -0.000072 -0.000067 0.017501 0.033502 -0.004130 -0.003844
KMI 0.000072 -0.000078 -0.000073 0.021165 0.003410 -0.003692 -0.003437
CHTR 0.001047 -0.000070 -0.000065 0.019267 0.054331 -0.003643 -0.003392
TFC 0.000371 -0.000058 -0.000054 0.018971 0.019544 -0.003050 -0.002839
URI 0.000990 -0.000074 -0.000069 0.029141 0.033968 -0.002548 -0.002372
CSX 0.001088 -0.000040 -0.000037 0.018954 0.057427 -0.002122 -0.001976
MCHP 0.000967 -0.000031 -0.000028 0.023195 0.041703 -0.001317 -0.001226
CPB 0.000056 -0.000020 -0.000018 0.018044 0.003121 -0.001096 -0.001020
BAC 0.000499 0.000021 0.000019 0.020456 0.024415 0.001006 0.000936
WFC -0.000369 0.000031 0.000029 0.019072 -0.019328 0.001620 0.001508
CVX 0.000106 0.000039 0.000036 0.017311 0.006112 0.002254 0.002098
USB 0.000129 0.000049 0.000046 0.016250 0.007952 0.003009 0.002801
VMC 0.000314 0.000068 0.000064 0.020520 0.015289 0.003325 0.003096
NUE 0.000253 0.000090 0.000084 0.021610 0.011698 0.004185 0.003896
DIS 0.000336 0.000085 0.000080 0.015915 0.021101 0.005369 0.004998
DE 0.000924 0.000123 0.000115 0.019988 0.046229 0.006163 0.005737
FCX 0.000840 0.000264 0.000246 0.039415 0.021303 0.006700 0.006237
AZO 0.000205 0.000123 0.000114 0.018225 0.011264 0.006746 0.006280
TMUS 0.000878 0.000151 0.000140 0.018355 0.047845 0.008206 0.007639
TGT 0.000635 0.000209 0.000195 0.021027 0.030187 0.009961 0.009273
MS 0.000452 0.000219 0.000204 0.020587 0.021975 0.010656 0.009920
MLM 0.000316 0.000246 0.000229 0.020894 0.015123 0.011792 0.010977
ELV 0.000518 0.000239 0.000222 0.019182 0.027023 0.012459 0.011598
ORLY 0.000200 0.000260 0.000242 0.018083 0.011035 0.014351 0.013359
PH 0.000461 0.000422 0.000393 0.019399 0.023780 0.021755 0.020252
GWW -0.000023 0.000704 0.000655 0.019939 -0.001139 0.035287 0.032848
FAST -0.000236 0.001089 0.001014 0.019667 -0.012004 0.055392 0.051565
DHR 0.000442 0.000869 0.000809 0.014023 0.031545 0.061991 0.057708
====================================================================================================
GH Mixing Distribution Parameters:
p: -5.000000e-01
a: 1.912434e+00
b: 1.657275e+00