This page was generated from a Jupyter notebook. You can view it on GitHub or download and run it locally.
S&P 500 Empirical Study: Distribution Comparison
This notebook compares various probability distributions for modeling S&P 500 daily log returns.
Distributions Compared
Normal - Baseline Gaussian distribution
Student-t - Heavy-tailed symmetric distribution
Variance Gamma (VG) - Normal-Gamma mixture, semi-heavy tails
Normal Inverse Gamma (NInvG) - Normal-InverseGamma mixture, heavy tails
Normal Inverse Gaussian (NIG) - Normal-InverseGaussian mixture
Generalized Hyperbolic (GH) - Most general, encompasses VG, NInvG, NIG as special cases
Stable (Lévy) - Power-law tails, potentially infinite variance
Methodology
Data: 10 years of S&P 500 daily returns
Training: First 5 years (in-sample)
Testing: Last 5 years (out-of-sample)
Metrics: KS test, Anderson-Darling test, tail fit analysis, QQ plots
[1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from scipy import stats
from scipy.stats import ks_2samp, anderson_ksamp
import warnings
warnings.filterwarnings('ignore')
# Import normix distributions
from normix.distributions.mixtures import (
VarianceGamma, NormalInverseGamma, NormalInverseGaussian, GeneralizedHyperbolic
)
plt.style.use('seaborn-v0_8-whitegrid')
%matplotlib inline
print("Imports successful!")
Imports successful!
1. Download and Prepare S&P 500 Data
[2]:
import yfinance as yf
from datetime import datetime, timedelta
# Download 10 years of S&P 500 data
end_date = datetime.now()
start_date = end_date - timedelta(days=365*10 + 30) # Extra buffer for trading days
print(f"Downloading S&P 500 data from {start_date.date()} to {end_date.date()}...")
sp500 = yf.download('^GSPC', start=start_date, end=end_date, progress=False)
print(f"Downloaded {len(sp500)} trading days")
print(f"Date range: {sp500.index[0].date()} to {sp500.index[-1].date()}")
Downloading S&P 500 data from 2016-01-12 to 2026-02-08...
Downloaded 2532 trading days
Date range: 2016-01-13 to 2026-02-06
[3]:
# Compute log returns
sp500['Log_Return'] = np.log(sp500['Close'] / sp500['Close'].shift(1))
sp500 = sp500.dropna()
# Split into training (first 5 years) and testing (last 5 years)
n_total = len(sp500)
n_train = n_total // 2
train_data = sp500.iloc[:n_train]
test_data = sp500.iloc[n_train:]
# Extract log returns as numpy arrays
returns_train = train_data['Log_Return'].values
returns_test = test_data['Log_Return'].values
print(f"\nTraining period: {train_data.index[0].date()} to {train_data.index[-1].date()}")
print(f"Training samples: {len(returns_train)}")
print(f"\nTesting period: {test_data.index[0].date()} to {test_data.index[-1].date()}")
print(f"Testing samples: {len(returns_test)}")
print(f"\n--- Training Data Statistics ---")
print(f"Mean: {returns_train.mean()*100:.4f}%")
print(f"Std: {returns_train.std()*100:.4f}%")
print(f"Skewness: {stats.skew(returns_train):.4f}")
print(f"Kurtosis: {stats.kurtosis(returns_train):.4f} (excess)")
print(f"Min: {returns_train.min()*100:.4f}%")
print(f"Max: {returns_train.max()*100:.4f}%")
Training period: 2016-01-14 to 2021-01-22
Training samples: 1265
Testing period: 2021-01-25 to 2026-02-06
Testing samples: 1266
--- Training Data Statistics ---
Mean: 0.0561%
Std: 1.2115%
Skewness: -1.1471
Kurtosis: 22.3473 (excess)
Min: -12.7652%
Max: 8.9683%
[4]:
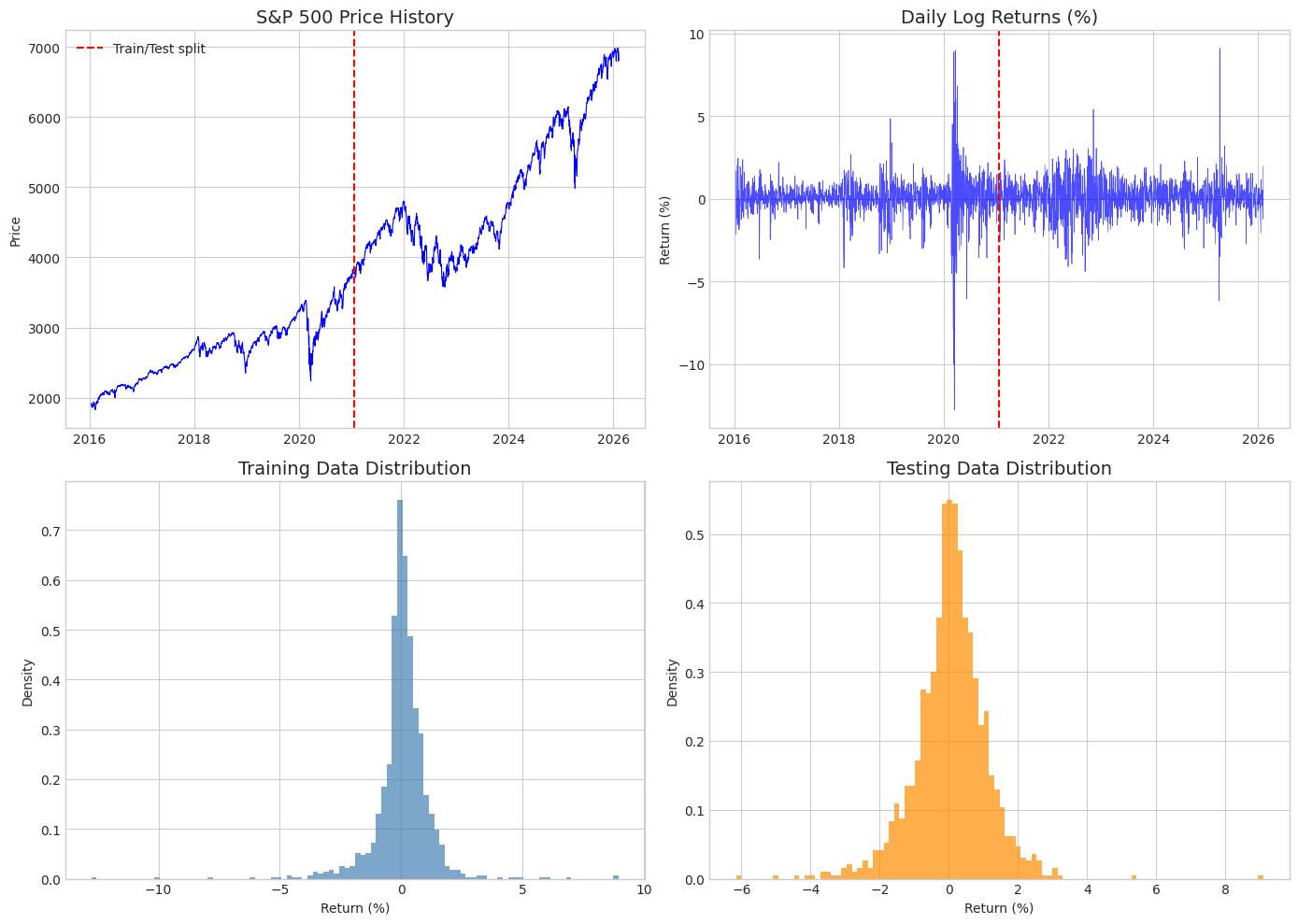
# Visualize the data
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# Price history
axes[0, 0].plot(sp500.index, sp500['Close'], 'b-', linewidth=0.8)
axes[0, 0].axvline(train_data.index[-1], color='red', linestyle='--', label='Train/Test split')
axes[0, 0].set_title('S&P 500 Price History', fontsize=14)
axes[0, 0].set_ylabel('Price')
axes[0, 0].legend()
# Returns time series
axes[0, 1].plot(sp500.index, sp500['Log_Return']*100, 'b-', linewidth=0.5, alpha=0.7)
axes[0, 1].axvline(train_data.index[-1], color='red', linestyle='--')
axes[0, 1].set_title('Daily Log Returns (%)', fontsize=14)
axes[0, 1].set_ylabel('Return (%)')
# Training histogram
axes[1, 0].hist(returns_train*100, bins=100, density=True, alpha=0.7, color='steelblue')
axes[1, 0].set_title('Training Data Distribution', fontsize=14)
axes[1, 0].set_xlabel('Return (%)')
axes[1, 0].set_ylabel('Density')
# Testing histogram
axes[1, 1].hist(returns_test*100, bins=100, density=True, alpha=0.7, color='darkorange')
axes[1, 1].set_title('Testing Data Distribution', fontsize=14)
axes[1, 1].set_xlabel('Return (%)')
axes[1, 1].set_ylabel('Density')
plt.tight_layout()
plt.show()
2. Fit Distributions to Training Data
We fit each distribution using Maximum Likelihood Estimation (MLE).
[5]:
# Reshape for normix (expects 2D input)
X_train = returns_train.reshape(-1, 1)
X_test = returns_test.reshape(-1, 1)
# Dictionary to store fitted distributions
fitted_dists = {}
print("Fitting distributions to training data...\n")
Fitting distributions to training data...
[6]:
# 1. Normal distribution
print("1. Fitting Normal distribution...")
mu_norm, std_norm = stats.norm.fit(returns_train)
fitted_dists['Normal'] = stats.norm(loc=mu_norm, scale=std_norm)
print(f" μ = {mu_norm:.6f}, σ = {std_norm:.6f}")
1. Fitting Normal distribution...
μ = 0.000561, σ = 0.012115
[7]:
# 2. Student-t distribution
print("2. Fitting Student-t distribution...")
df_t, loc_t, scale_t = stats.t.fit(returns_train)
fitted_dists['Student-t'] = stats.t(df=df_t, loc=loc_t, scale=scale_t)
print(f" df = {df_t:.4f}, loc = {loc_t:.6f}, scale = {scale_t:.6f}")
2. Fitting Student-t distribution...
df = 1.9546, loc = 0.001006, scale = 0.005114
[9]:
# 3. Variance Gamma
print("3. Fitting Variance Gamma distribution (EM algorithm)...")
vg = VarianceGamma()
vg.fit(X_train, max_iter=100, tol=1e-6, verbose=0)
fitted_dists['Variance Gamma'] = vg
vg_params = vg.classical_params
print(f" μ = {vg_params.mu[0]:.6f}, γ = {vg_params.gamma[0]:.6f}")
print(f" σ² = {vg_params.sigma[0,0]:.8f}, α = {vg_params.shape:.4f}, β = {vg_params.rate:.4f}")
3. Fitting Variance Gamma distribution (EM algorithm)...
μ = 0.001560, γ = -0.000511
σ² = 0.00005560, α = 0.6843, β = 0.3497
[10]:
# 4. Normal Inverse Gamma
print("4. Fitting Normal Inverse Gamma distribution (EM algorithm)...")
ninvg = NormalInverseGamma()
ninvg.fit(X_train, max_iter=100, tol=1e-6, verbose=0)
fitted_dists['Normal Inv Gamma'] = ninvg
ninvg_params = ninvg.classical_params
print(f" μ = {ninvg_params.mu[0]:.6f}, γ = {ninvg_params.gamma[0]:.6f}")
print(f" σ² = {ninvg_params.sigma[0,0]:.8f}, α = {ninvg_params.shape:.4f}, β = {ninvg_params.rate:.4f}")
4. Fitting Normal Inverse Gamma distribution (EM algorithm)...
μ = 0.001416, γ = -0.000885
σ² = 0.00012349, α = 1.5000, β = 0.4245
[11]:
# 5. Normal Inverse Gaussian
print("5. Fitting Normal Inverse Gaussian distribution (EM algorithm)...")
nig = NormalInverseGaussian()
nig.fit(X_train, max_iter=100, tol=1e-6, verbose=0)
fitted_dists['Normal Inv Gaussian'] = nig
nig_params = nig.classical_params
print(f" μ = {nig_params.mu[0]:.6f}, γ = {nig_params.gamma[0]:.6f}")
print(f" σ² = {nig_params.sigma[0,0]:.8f}, δ = {nig_params.delta:.6f}, η = {nig_params.eta:.6f}")
5. Fitting Normal Inverse Gaussian distribution (EM algorithm)...
μ = 0.001057, γ = -0.000265
σ² = 0.00007264, δ = 1.876384, η = 0.343700
[12]:
# 6. Generalized Hyperbolic
print("6. Fitting Generalized Hyperbolic distribution (EM algorithm)...")
gh = GeneralizedHyperbolic()
# Use fix_p regularization with p=-0.5 (NIG-like) for stability on return data
gh.fit(X_train, max_iter=100, tol=1e-4, verbose=0,
regularization='fix_p', regularization_params={'p_fixed': -0.5})
fitted_dists['Gen. Hyperbolic'] = gh
gh_params = gh.classical_params
print(f" μ = {gh_params.mu[0]:.6f}, γ = {gh_params.gamma[0]:.6f}")
print(f" σ² = {gh_params.sigma[0,0]:.8f}")
print(f" p = {gh_params.p:.4f}, a = {gh_params.a:.4f}, b = {gh_params.b:.4f}")
6. Fitting Generalized Hyperbolic distribution (EM algorithm)...
μ = 0.001059, γ = -0.000017
σ² = 0.00000480
p = -0.5000, a = 0.0057, b = 5.3788
[13]:
# 7. Stable (Lévy) distribution
print("7. Fitting Stable (Lévy) distribution...")
print(" (This may take a while...)")
alpha_s, beta_s, loc_s, scale_s = stats.levy_stable.fit(returns_train)
fitted_dists['Stable'] = stats.levy_stable(alpha=alpha_s, beta=beta_s, loc=loc_s, scale=scale_s)
print(f" α = {alpha_s:.4f}, β = {beta_s:.4f}, loc = {loc_s:.6f}, scale = {scale_s:.6f}")
print("\nAll distributions fitted!")
7. Fitting Stable (Lévy) distribution...
(This may take a while...)
α = 1.3849, β = -0.0358, loc = 0.000903, scale = 0.004409
All distributions fitted!
3. In-Sample Comparison (Training Data)
[14]:
def get_pdf_values(dist, x, dist_name):
"""Get PDF values for a distribution (handles both scipy and normix)."""
if dist_name in ['Normal', 'Student-t', 'Stable']:
return dist.pdf(x)
else:
# normix distributions expect 2D input
return dist.pdf(x.reshape(-1, 1)).flatten()
def generate_samples(dist, n_samples, dist_name, random_state=42):
"""Generate samples from a distribution."""
if dist_name in ['Normal', 'Student-t', 'Stable']:
return dist.rvs(size=n_samples, random_state=random_state)
else:
return dist.rvs(size=n_samples, random_state=random_state).flatten()
[15]:
# Define x range for PDF plotting
x_range = np.linspace(returns_train.min() * 1.2, returns_train.max() * 1.2, 500)
# Colors for each distribution
colors = {
'Normal': 'blue',
'Student-t': 'red',
'Variance Gamma': 'green',
'Normal Inv Gamma': 'purple',
'Normal Inv Gaussian': 'orange',
'Gen. Hyperbolic': 'brown',
'Stable': 'cyan'
}
[16]:
# Plot all distributions against training data histogram
fig, axes = plt.subplots(1, 2, figsize=(16, 6))
# Linear scale
axes[0].hist(returns_train, bins=100, density=True, alpha=0.5, color='gray', label='Data')
for name, dist in fitted_dists.items():
pdf_vals = get_pdf_values(dist, x_range, name)
axes[0].plot(x_range, pdf_vals, color=colors[name], linewidth=1.5, label=name)
axes[0].set_xlabel('Log Return', fontsize=12)
axes[0].set_ylabel('Density', fontsize=12)
axes[0].set_title('In-Sample: PDF Comparison (Linear Scale)', fontsize=14)
axes[0].legend(loc='upper right', fontsize=9)
axes[0].set_xlim(returns_train.min() * 1.1, returns_train.max() * 1.1)
# Log scale for tail comparison
axes[1].hist(returns_train, bins=100, density=True, alpha=0.5, color='gray', label='Data')
for name, dist in fitted_dists.items():
pdf_vals = get_pdf_values(dist, x_range, name)
pdf_vals = np.clip(pdf_vals, 1e-10, None) # Avoid log(0)
axes[1].semilogy(x_range, pdf_vals, color=colors[name], linewidth=1.5, label=name)
axes[1].set_xlabel('Log Return', fontsize=12)
axes[1].set_ylabel('Density (log scale)', fontsize=12)
axes[1].set_title('In-Sample: Tail Comparison (Log Scale)', fontsize=14)
axes[1].legend(loc='upper right', fontsize=9)
axes[1].set_xlim(returns_train.min() * 1.1, returns_train.max() * 1.1)
axes[1].set_ylim(1e-4, None)
plt.tight_layout()
plt.show()
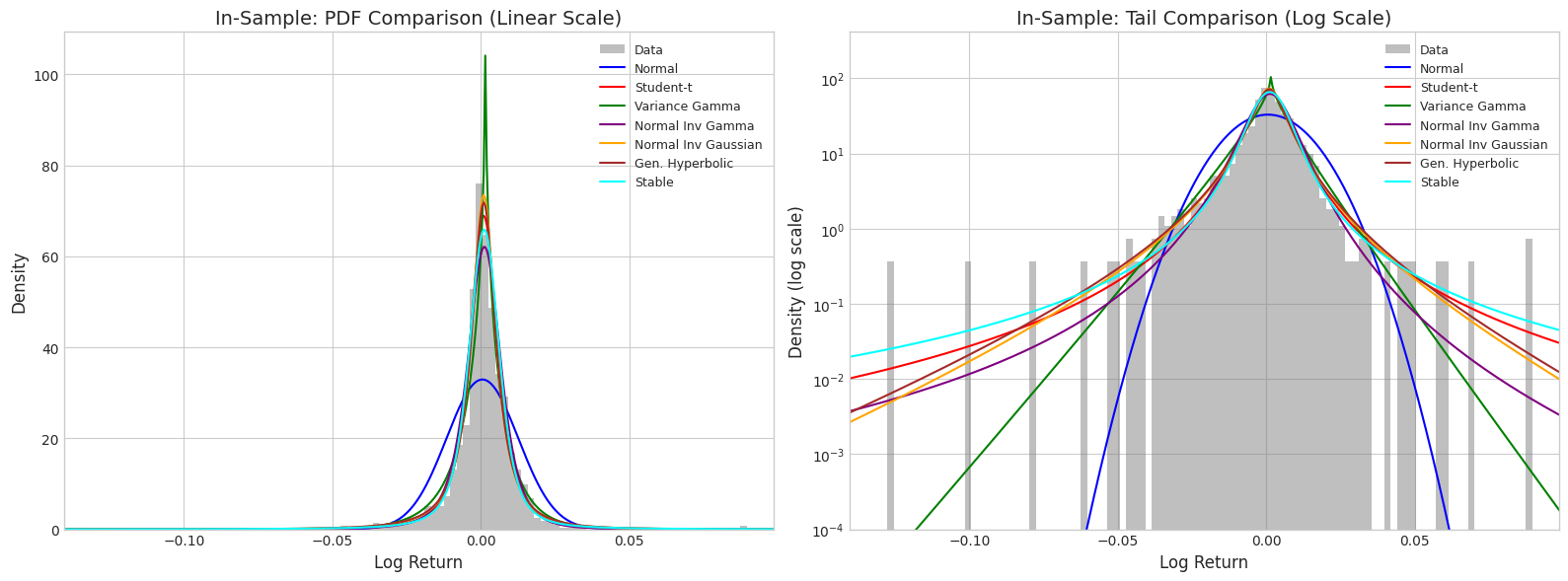
4. Out-of-Sample Comparison (Testing Data)
[17]:
# Plot all distributions against testing data histogram
x_range_test = np.linspace(returns_test.min() * 1.2, returns_test.max() * 1.2, 500)
fig, axes = plt.subplots(1, 2, figsize=(16, 6))
# Linear scale
axes[0].hist(returns_test, bins=100, density=True, alpha=0.5, color='gray', label='Test Data')
for name, dist in fitted_dists.items():
pdf_vals = get_pdf_values(dist, x_range_test, name)
axes[0].plot(x_range_test, pdf_vals, color=colors[name], linewidth=1.5, label=name)
axes[0].set_xlabel('Log Return', fontsize=12)
axes[0].set_ylabel('Density', fontsize=12)
axes[0].set_title('Out-of-Sample: PDF Comparison (Linear Scale)', fontsize=14)
axes[0].legend(loc='upper right', fontsize=9)
axes[0].set_xlim(returns_test.min() * 1.1, returns_test.max() * 1.1)
# Log scale for tail comparison
axes[1].hist(returns_test, bins=100, density=True, alpha=0.5, color='gray', label='Test Data')
for name, dist in fitted_dists.items():
pdf_vals = get_pdf_values(dist, x_range_test, name)
pdf_vals = np.clip(pdf_vals, 1e-10, None)
axes[1].semilogy(x_range_test, pdf_vals, color=colors[name], linewidth=1.5, label=name)
axes[1].set_xlabel('Log Return', fontsize=12)
axes[1].set_ylabel('Density (log scale)', fontsize=12)
axes[1].set_title('Out-of-Sample: Tail Comparison (Log Scale)', fontsize=14)
axes[1].legend(loc='upper right', fontsize=9)
axes[1].set_xlim(returns_test.min() * 1.1, returns_test.max() * 1.1)
axes[1].set_ylim(1e-4, None)
plt.tight_layout()
plt.show()
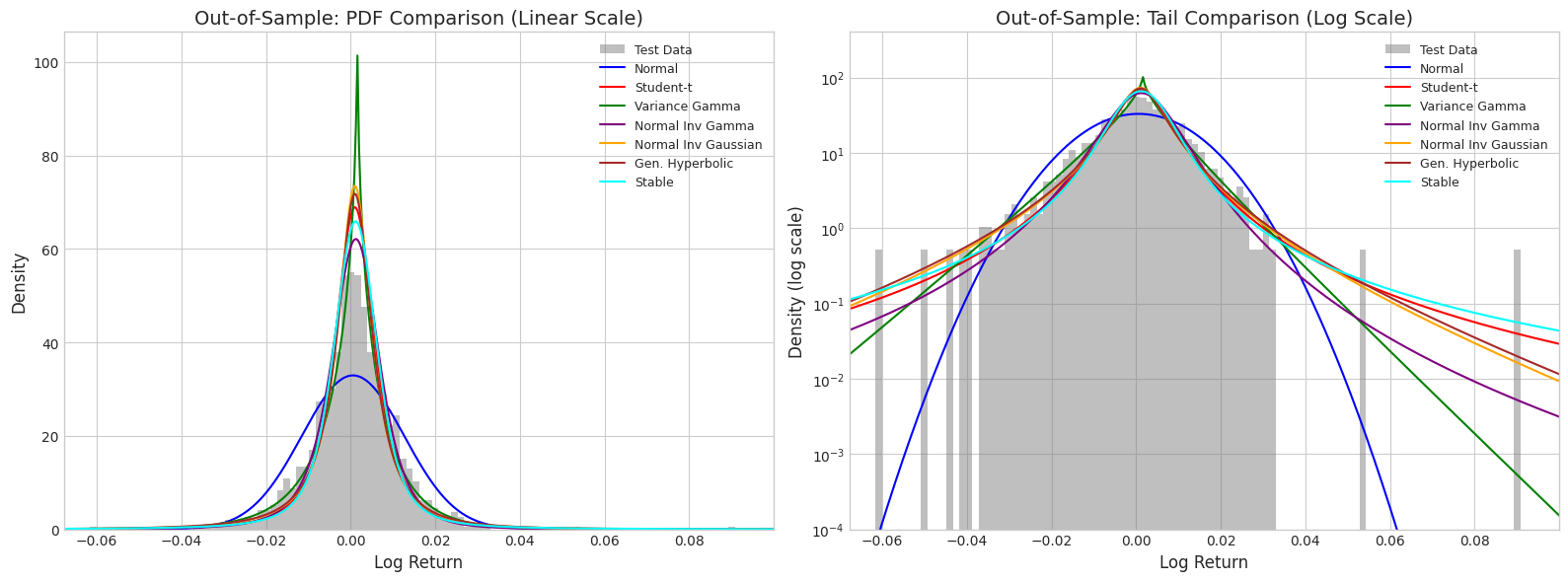
5. Statistical Tests
5.1 Kolmogorov-Smirnov Test (Two-Sample)
We compare samples generated from each fitted distribution against the actual data.
[18]:
# Generate samples from each distribution for testing
n_sim = 100000
print("Kolmogorov-Smirnov Two-Sample Test")
print("="*70)
print(f"{'Distribution':<20} {'In-Sample KS':<15} {'p-value':<12} {'Out-Sample KS':<15} {'p-value':<12}")
print("-"*70)
ks_results = {}
for name, dist in fitted_dists.items():
# Generate samples from fitted distribution
sim_samples = generate_samples(dist, n_sim, name)
# In-sample test
ks_in, pval_in = ks_2samp(returns_train, sim_samples)
# Out-of-sample test
ks_out, pval_out = ks_2samp(returns_test, sim_samples)
ks_results[name] = {
'ks_in': ks_in, 'pval_in': pval_in,
'ks_out': ks_out, 'pval_out': pval_out
}
print(f"{name:<20} {ks_in:<15.4f} {pval_in:<12.4f} {ks_out:<15.4f} {pval_out:<12.4f}")
print("\nNote: Lower KS statistic = better fit. p-value > 0.05 suggests distributions are similar.")
Kolmogorov-Smirnov Two-Sample Test
======================================================================
Distribution In-Sample KS p-value Out-Sample KS p-value
----------------------------------------------------------------------
Normal 0.1556 0.0000 0.0863 0.0000
Student-t 0.0277 0.2885 0.0636 0.0001
Variance Gamma 0.0462 0.0093 0.0497 0.0040
Normal Inv Gamma 0.0387 0.0466 0.0528 0.0018
Normal Inv Gaussian 0.0291 0.2371 0.0582 0.0004
Gen. Hyperbolic 0.0283 0.2636 0.0537 0.0014
Stable 0.0363 0.0730 0.0619 0.0001
Note: Lower KS statistic = better fit. p-value > 0.05 suggests distributions are similar.
5.2 Anderson-Darling Test (Two-Sample)
The Anderson-Darling test is more sensitive to the tails than KS.
[19]:
print("Anderson-Darling Two-Sample Test")
print("="*70)
print(f"{'Distribution':<20} {'In-Sample AD':<15} {'Out-Sample AD':<15} {'Critical 5%':<15}")
print("-"*70)
ad_results = {}
for name, dist in fitted_dists.items():
# Generate samples from fitted distribution
sim_samples = generate_samples(dist, n_sim, name)
# In-sample test
ad_in = anderson_ksamp([returns_train, sim_samples])
# Out-of-sample test
ad_out = anderson_ksamp([returns_test, sim_samples])
ad_results[name] = {
'ad_in': ad_in.statistic, 'ad_out': ad_out.statistic,
'critical': ad_in.critical_values[2] # 5% significance level
}
print(f"{name:<20} {ad_in.statistic:<15.4f} {ad_out.statistic:<15.4f} {ad_in.critical_values[2]:<15.4f}")
print("\nNote: Lower AD statistic = better fit. Statistic < Critical value suggests good fit.")
Anderson-Darling Two-Sample Test
======================================================================
Distribution In-Sample AD Out-Sample AD Critical 5%
----------------------------------------------------------------------
Normal 70.7082 30.1942 1.9610
Student-t 0.2328 12.8847 1.9610
Variance Gamma 3.1342 4.7024 1.9610
Normal Inv Gamma 2.2997 9.4993 1.9610
Normal Inv Gaussian 0.3292 11.8352 1.9610
Gen. Hyperbolic 0.4668 9.0548 1.9610
Stable 0.8099 12.5652 1.9610
Note: Lower AD statistic = better fit. Statistic < Critical value suggests good fit.
6. Tail Analysis
6.1 Empirical vs Fitted Tail Probabilities
[20]:
def get_cdf_values(dist, x, dist_name):
"""Get CDF values for a distribution."""
if dist_name in ['Normal', 'Student-t', 'Stable']:
return dist.cdf(x)
else:
# For normix, compute CDF by numerical integration or use empirical
samples = generate_samples(dist, 50000, dist_name, random_state=123)
return np.array([np.mean(samples <= xi) for xi in x])
# Compute tail probabilities at various quantiles
tail_quantiles = [0.01, 0.025, 0.05, 0.95, 0.975, 0.99]
print("Tail Probability Comparison (Out-of-Sample)")
print("="*90)
print(f"{'Quantile':<10}", end="")
print(f"{'Empirical':<12}", end="")
for name in fitted_dists.keys():
print(f"{name[:10]:<12}", end="")
print()
print("-"*90)
# Compute empirical quantiles from test data
empirical_quantiles = np.quantile(returns_test, tail_quantiles)
for i, q in enumerate(tail_quantiles):
emp_val = empirical_quantiles[i]
print(f"{q:<10.3f}", end="")
print(f"{emp_val:<12.6f}", end="")
for name, dist in fitted_dists.items():
if name in ['Normal', 'Student-t', 'Stable']:
fitted_val = dist.ppf(q)
else:
# Use simulation for normix distributions
samples = generate_samples(dist, 50000, name, random_state=456)
fitted_val = np.quantile(samples, q)
print(f"{fitted_val:<12.6f}", end="")
print()
Tail Probability Comparison (Out-of-Sample)
==========================================================================================
Quantile Empirical Normal Student-t Variance G Normal Inv Normal Inv Gen. Hyper Stable
------------------------------------------------------------------------------------------
0.010 -0.029946 -0.027623 -0.035759 -0.031969 -0.028867 -0.038152 -0.039797 -0.044184
0.025 -0.021651 -0.023184 -0.021495 -0.023617 -0.019301 -0.024392 -0.025947 -0.023197
0.050 -0.016600 -0.019367 -0.014166 -0.017294 -0.013759 -0.016397 -0.017029 -0.014355
0.950 0.016196 0.020488 0.016179 0.016404 0.014096 0.016167 0.016583 0.015858
0.975 0.020344 0.024305 0.023508 0.021478 0.018144 0.023294 0.023512 0.024179
0.990 0.025119 0.028744 0.037772 0.028384 0.025031 0.033517 0.034526 0.044019
6.2 QQ Plots
[21]:
def make_qq_plot(ax, data, dist, dist_name, title):
"""Create QQ plot comparing data to fitted distribution."""
n = len(data)
sorted_data = np.sort(data)
theoretical_quantiles = np.linspace(0.001, 0.999, n)
if dist_name in ['Normal', 'Student-t', 'Stable']:
theoretical_values = dist.ppf(theoretical_quantiles)
else:
# Use simulation for normix
samples = generate_samples(dist, 50000, dist_name, random_state=789)
theoretical_values = np.quantile(samples, theoretical_quantiles)
ax.scatter(theoretical_values, sorted_data, alpha=0.3, s=5)
# Add 45-degree line
lims = [min(theoretical_values.min(), sorted_data.min()),
max(theoretical_values.max(), sorted_data.max())]
ax.plot(lims, lims, 'r--', linewidth=1.5, label='Perfect fit')
ax.set_xlabel('Theoretical Quantiles', fontsize=10)
ax.set_ylabel('Sample Quantiles', fontsize=10)
ax.set_title(title, fontsize=11)
ax.legend(loc='lower right', fontsize=8)
# Create QQ plots for out-of-sample data
fig, axes = plt.subplots(2, 4, figsize=(16, 10))
axes = axes.flatten()
for i, (name, dist) in enumerate(fitted_dists.items()):
make_qq_plot(axes[i], returns_test, dist, name, f'QQ Plot: {name}')
# Hide empty subplot
axes[-1].axis('off')
plt.suptitle('Out-of-Sample QQ Plots', fontsize=14, y=1.02)
plt.tight_layout()
plt.show()
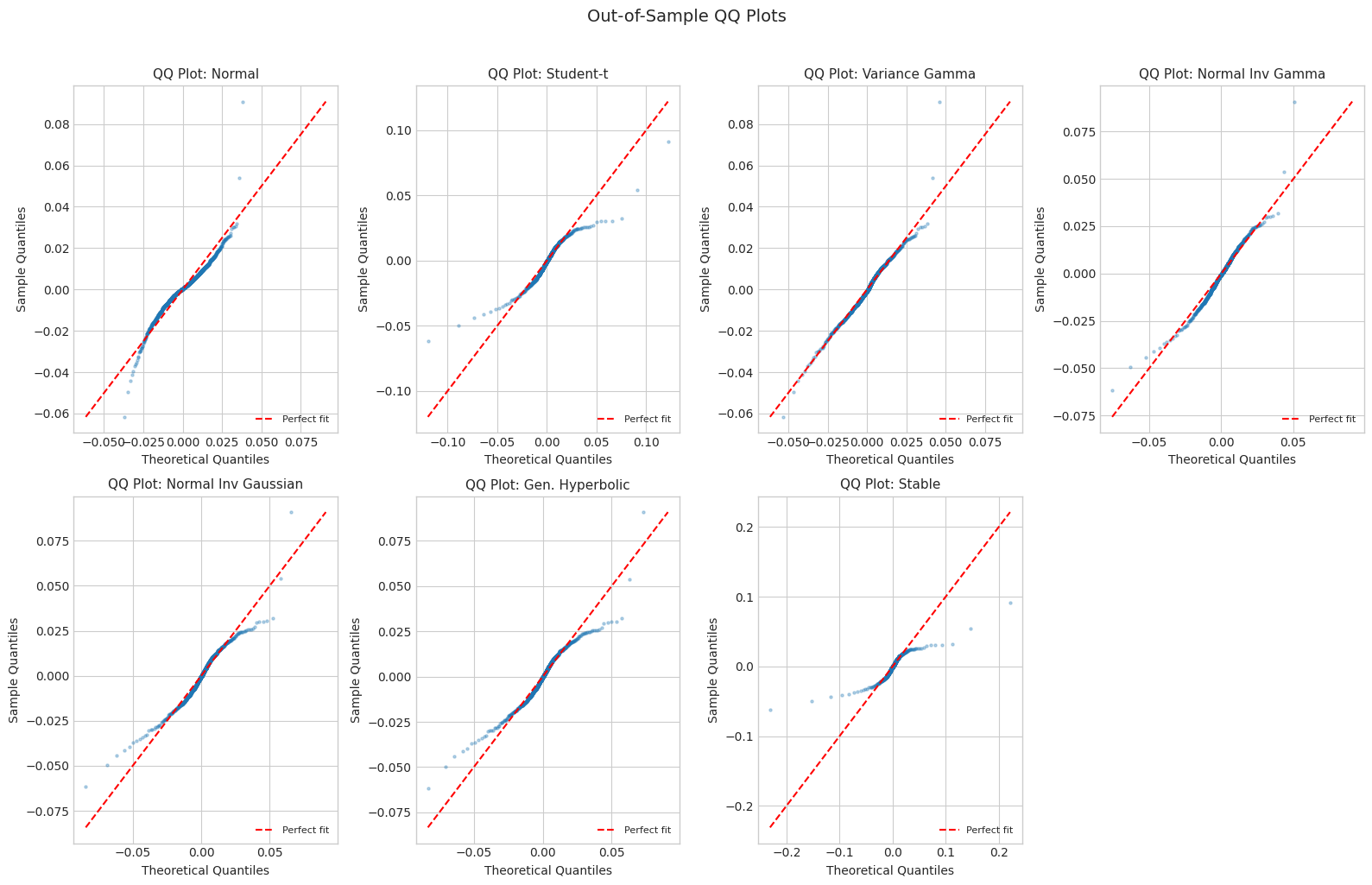
6.3 Tail Index Estimation (Hill Estimator)
The Hill estimator estimates the tail index \(\alpha\) for heavy-tailed distributions. For data with power-law tails: \(P(X > x) \sim x^{-\alpha}\)
[22]:
def hill_estimator(data, k):
"""Hill estimator for tail index using top k order statistics."""
sorted_data = np.sort(np.abs(data))[::-1] # Sort descending by absolute value
if k >= len(data) or k < 1:
return np.nan
log_ratios = np.log(sorted_data[:k]) - np.log(sorted_data[k])
return k / np.sum(log_ratios)
# Compute Hill estimator for different k values
k_values = np.arange(10, 200, 5)
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
# Left tail (negative returns)
left_tail_train = -returns_train[returns_train < 0]
left_tail_test = -returns_test[returns_test < 0]
hill_left_train = [hill_estimator(left_tail_train, k) for k in k_values]
hill_left_test = [hill_estimator(left_tail_test, k) for k in k_values]
axes[0].plot(k_values, hill_left_train, 'b-', linewidth=2, label='Training')
axes[0].plot(k_values, hill_left_test, 'r--', linewidth=2, label='Testing')
axes[0].axhline(y=3, color='gray', linestyle=':', label='α=3 (finite variance)')
axes[0].axhline(y=2, color='gray', linestyle='-.', label='α=2 (finite mean)')
axes[0].set_xlabel('Number of order statistics (k)', fontsize=12)
axes[0].set_ylabel('Tail index α', fontsize=12)
axes[0].set_title('Left Tail (Losses) - Hill Estimator', fontsize=14)
axes[0].legend()
axes[0].set_ylim(0, 6)
# Right tail (positive returns)
right_tail_train = returns_train[returns_train > 0]
right_tail_test = returns_test[returns_test > 0]
hill_right_train = [hill_estimator(right_tail_train, k) for k in k_values]
hill_right_test = [hill_estimator(right_tail_test, k) for k in k_values]
axes[1].plot(k_values, hill_right_train, 'b-', linewidth=2, label='Training')
axes[1].plot(k_values, hill_right_test, 'r--', linewidth=2, label='Testing')
axes[1].axhline(y=3, color='gray', linestyle=':', label='α=3')
axes[1].axhline(y=2, color='gray', linestyle='-.', label='α=2')
axes[1].set_xlabel('Number of order statistics (k)', fontsize=12)
axes[1].set_ylabel('Tail index α', fontsize=12)
axes[1].set_title('Right Tail (Gains) - Hill Estimator', fontsize=14)
axes[1].legend()
axes[1].set_ylim(0, 6)
plt.tight_layout()
plt.show()
# Estimate stable tail index (using k=50)
k_stable = 50
print(f"\nHill Tail Index Estimates (k={k_stable}):")
print(f" Left tail (losses): Train={hill_estimator(left_tail_train, k_stable):.3f}, Test={hill_estimator(left_tail_test, k_stable):.3f}")
print(f" Right tail (gains): Train={hill_estimator(right_tail_train, k_stable):.3f}, Test={hill_estimator(right_tail_test, k_stable):.3f}")
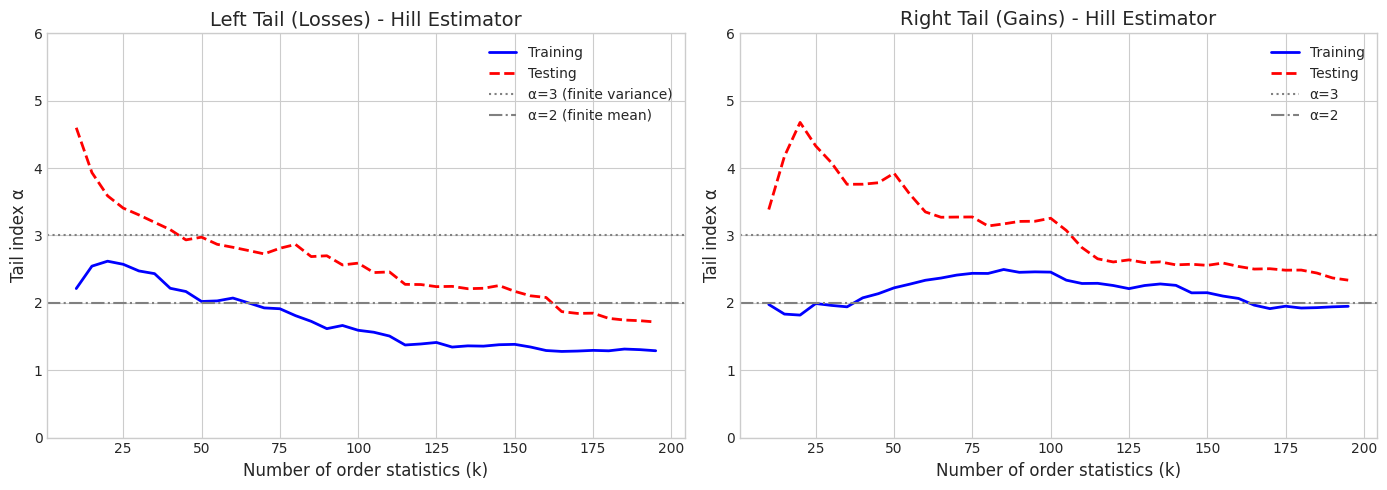
Hill Tail Index Estimates (k=50):
Left tail (losses): Train=2.020, Test=2.975
Right tail (gains): Train=2.222, Test=3.924
7. Value at Risk (VaR) Backtesting
[23]:
def compute_var(dist, alpha, dist_name):
"""Compute Value at Risk at level alpha."""
if dist_name in ['Normal', 'Student-t', 'Stable']:
return dist.ppf(alpha)
else:
samples = generate_samples(dist, 100000, dist_name, random_state=999)
return np.quantile(samples, alpha)
# VaR levels to test
var_levels = [0.01, 0.025, 0.05]
print("Value at Risk Backtesting (Out-of-Sample)")
print("="*80)
for alpha in var_levels:
print(f"\nVaR at {alpha*100:.1f}% level (Expected exceedances: {alpha*100:.1f}%)")
print("-"*60)
print(f"{'Distribution':<20} {'VaR':<15} {'Exceedances':<15} {'Rate (%)':<12}")
print("-"*60)
for name, dist in fitted_dists.items():
var = compute_var(dist, alpha, name)
exceedances = np.sum(returns_test < var)
rate = exceedances / len(returns_test) * 100
print(f"{name:<20} {var:<15.6f} {exceedances:<15d} {rate:<12.2f}")
Value at Risk Backtesting (Out-of-Sample)
================================================================================
VaR at 1.0% level (Expected exceedances: 1.0%)
------------------------------------------------------------
Distribution VaR Exceedances Rate (%)
------------------------------------------------------------
Normal -0.027623 18 1.42
Student-t -0.035759 7 0.55
Variance Gamma -0.031548 11 0.87
Normal Inv Gamma -0.028953 15 1.18
Normal Inv Gaussian -0.037818 5 0.39
Gen. Hyperbolic -0.039606 4 0.32
Stable -0.044184 3 0.24
VaR at 2.5% level (Expected exceedances: 2.5%)
------------------------------------------------------------
Distribution VaR Exceedances Rate (%)
------------------------------------------------------------
Normal -0.023184 29 2.29
Student-t -0.021495 33 2.61
Variance Gamma -0.023377 29 2.29
Normal Inv Gamma -0.019077 47 3.71
Normal Inv Gaussian -0.024124 25 1.97
Gen. Hyperbolic -0.025413 21 1.66
Stable -0.023197 29 2.29
VaR at 5.0% level (Expected exceedances: 5.0%)
------------------------------------------------------------
Distribution VaR Exceedances Rate (%)
------------------------------------------------------------
Normal -0.019367 44 3.48
Student-t -0.014166 94 7.42
Variance Gamma -0.017301 58 4.58
Normal Inv Gamma -0.013496 103 8.14
Normal Inv Gaussian -0.016315 67 5.29
Gen. Hyperbolic -0.016705 62 4.90
Stable -0.014355 93 7.35
[ ]: